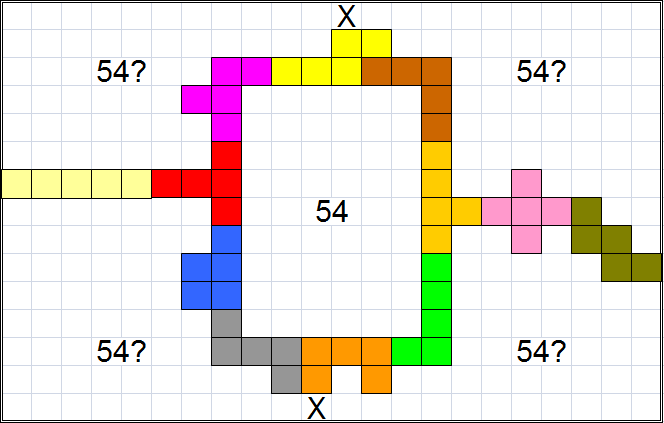
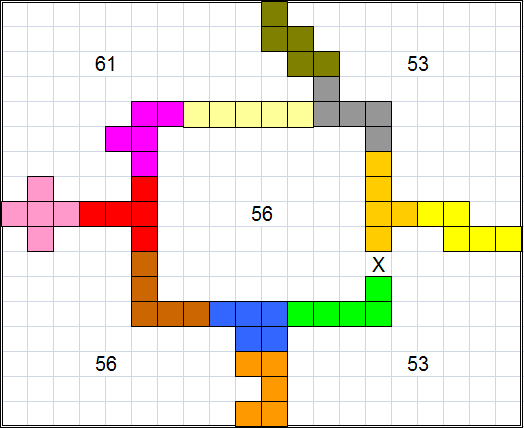
Try to place the 12 pentominoes inside the largest possible rectangle, in such a way
that the pentominoes divide the rectangle in 5 parts of equal size.
There may not be more then 5 open areas; also open areas are not allowed to
touch each other in a corner.
The pentominoes must form one shape, so that from any pentomino there is a
pentomino path to any other pentomino.
Find the largest solution in which there is a rectangle in the centre, enclosed
by pentominoes.
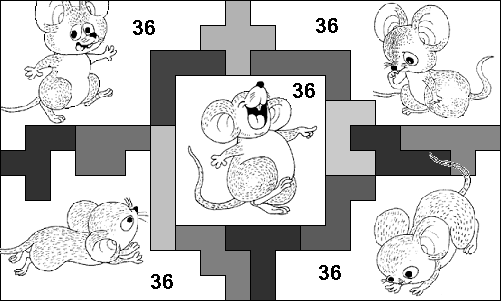
The parts in our example are 36 squares.
The rectangle is even a square.