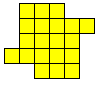
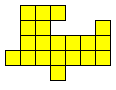
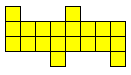
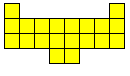
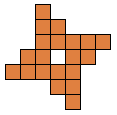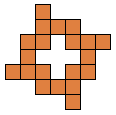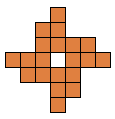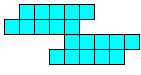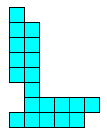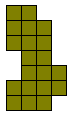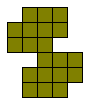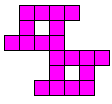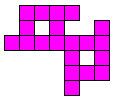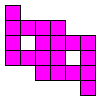Congruentie en PentoMeerlingen
Patrick Hamlyn publiceerde op
Polyforms pentominoduo's als antwoord op Robert Reid.
Hij tekende
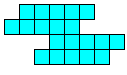
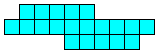
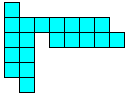
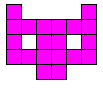
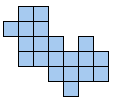
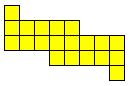
alle vormen die men kan maken met 2 congruente pentomino's.
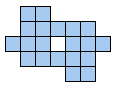
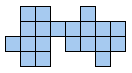
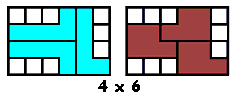
Bijna gelijktijdig kregen we van
Aad van de Wetering een PP-voorstelling met alle congruente vormen die men kan maken met 2 congruente pentomino's.
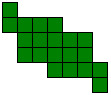
De figuren (in totaal 22) zijn ingedeeld naargelang de afmetingen van de omgesloten rechthoek.
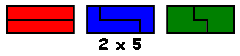
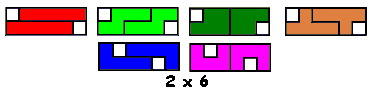
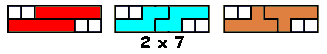

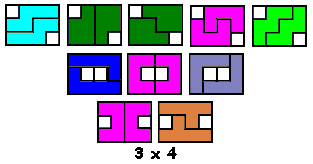
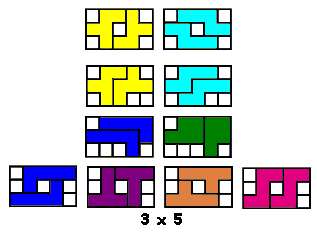
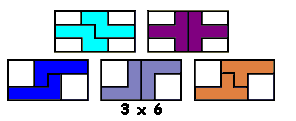


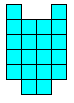
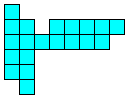
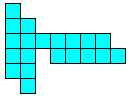
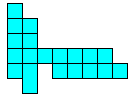
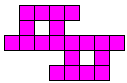
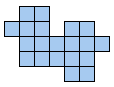
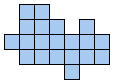
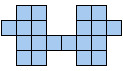
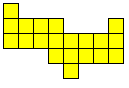
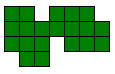
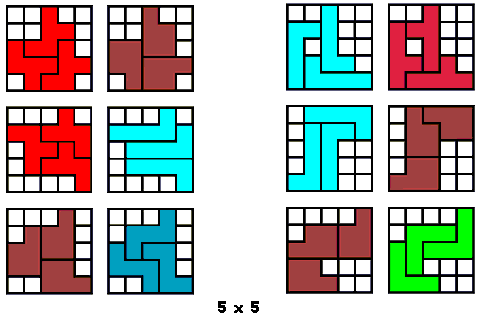
Het is logisch dat we dit uitbreiden naar het zoeken van alle congruente vormen die men kan maken met 3 congruente pentomino's. Patrick Hamlyn plaatste de 20 vormen bij elkaar.
Aad van de Wetering ordende de 20 figuren naargelang de afmetingen van de omgesloten rechthoek.
Erich Friedman maakte hiermee een puzzel
"Polyomino Addition Puzzles". De orange vormen vinden we zelf de leukste omdat deze niet afkomstig zijn van 2 pentominoduo's.
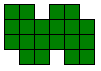
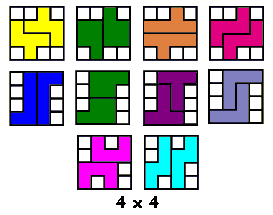
Jorge Mireles publiceerde op
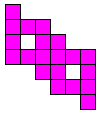
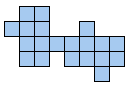
Polyforms 10 van de 20 vormen die hij zelf gevonden had (zonder computerhulp). Kan jij dit beter?
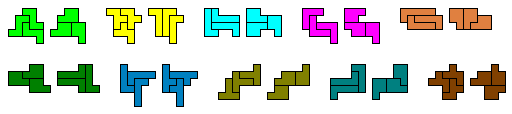
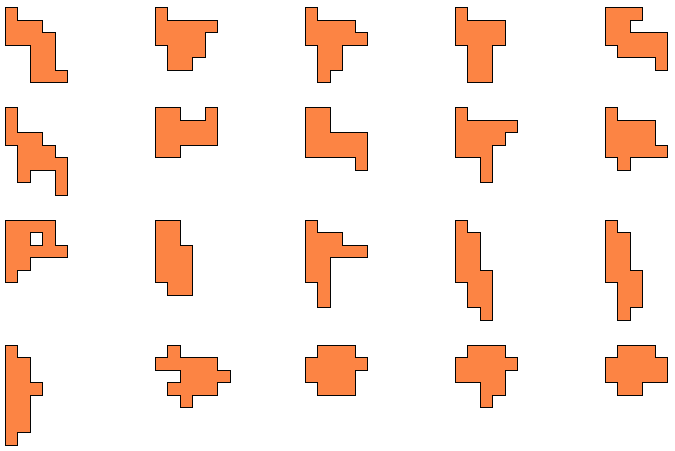
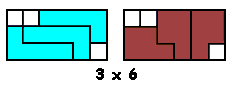
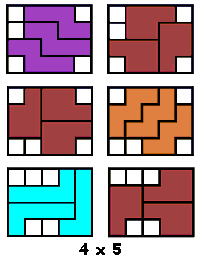
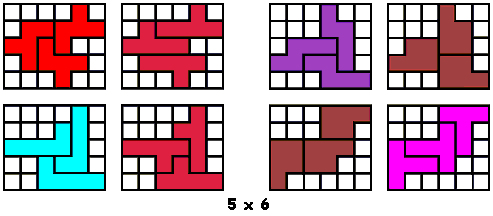
Hij vraagt naar vormen die enerzijds te vullen zijn met 3 gelijke pentomino's en
anderzijds met 3 dezelfde vormen van een andere pentomino. Hij wil dat de
oplossing enig is.
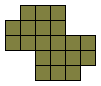
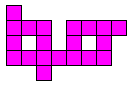
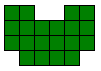
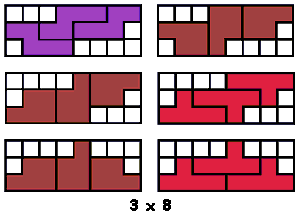
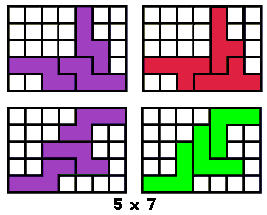
Hij heeft echter nog zes andere opgaven.
Zoek telkens de vorm die te vullen is met 2I 1Y en 1I 2Y, 2L 1U en 1L 2U, 2F 1U
en 1F 2U, 2N 1W en 1N 2W, 2L 1W en 1L 2W, 2L 1F en 1L 2F. De oplossingen kan je
op de bovengenoemde site vinden.
En we zijn niet te stuiten.
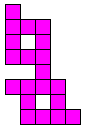
We wilden alle congruente vormen zoeken gevormd door 4 congruente pentomino's
Na lezen van wat Patrick Hamlyn mailde:"Here are the counts for distinct shapes made from four copies of each pentomino, made by Peter's program DYNPOL.
F 338351, I 3913, L 697931, N 494164, P 313096, T 31743, U 30614, V 41975, W 21936, X 569, Y 498647, Z 70649" zagen we het niet doenbaar.
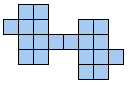
Patrick publiceerde echter alle 156
quadruples=vormen waarbij er keuze is uit 4 verschillende pentomino's om ze te vullen met 4 congruente.
We tekenden bij elke vorm de mogelijke oplossingen. Klik hiervoor op de vorm.
Commentaar is altijd welkom.
o.d.m@fulladsl.be