Omtrek I-pentomino

 Het idee van de vraag komt uit de Vlaamse Wiskunde Olympiade 1998-1999, Tweede Ronde.

Elk vierkant van de I-pentomino wordt verdeeld in 7 congruente rechthoeken met elk een omtrek van 32 cm.

Wat is de omtrek van de I-pentomino?

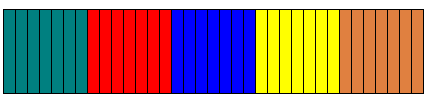
Hulp:

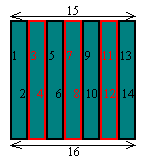
We zien dat de som van de omtrekken van de 7 rechthoeken gelijk is aan 16x zijde van een vierkant van de I-pentomino.

Oplossing:

Omtrek 7 rechthoeken is 32cm x 7 = 224 cm

De zijde van een vierkant is 224 cm : 16 = 14 cm

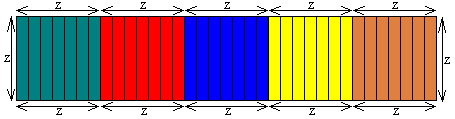
De omtrek van de I-pentomino is 14 cm x 12 = 168 cm

Aad van de Wetering mailde ons een andere manier om het probleem te bekijken:

Stel zijde vierkant I-pento = x; x is ook de lengte van de lange zijde van de rechthoek. De korte zijde is 1/7 van de lange zijde. De omtrek van de rechthoek is 2x + 2/7 x. Gegeven is dat de omtrek 32 cm is, dus x = 14 cm.

Omtrek I-pentomino: 12 x 14 cm = 168 cm.