https://www.youtube.com/user/EdoTimmermans?feature=mhee
The tetrominoset is made with ningboballs that you can buy at
http://www.ningboballs.eu/en/
You get a set of tetrominoes
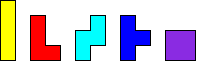
With this set you can make the base form in 8 different ways.

Below you can see how this is possible.

Solution 1 and 2 form slightly different cilinder.
Solution 3A and 3B form the same cilinder.
Solution 4A and 4B form the same cilinder.
Solution 5 and 6 form slightly different cilinder.
Solutions 1,2,3,4,5 and 6 all fit in the base shape that forms the cilinder.
Solution 7 is the only solution that can not fit in this base shape and still forms the same tube.
Can you find it?
Martin Grider made a video with the following solution

We explain why this solution is not new: it fits in the base shape.
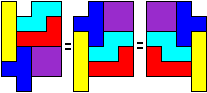
Helmut Postl sent us the solution and the following beautiful statement: "An interesting fact is that there are different cylinders as well, but none of those can be built by the tetrominoes. The actual cylinder has height h=4 and circumference c=5. In principle, you can build cylinders with h*c=20, that is (h,c) = (1,20), (2,10), (4,5), (5,4), (10,2) and (20,1). Since the tetrominoes have odd checkerboard parity, the circumference must be odd. This leaves (4,5) and (20,1), where the latter of course cannot be built by the tetrominoes."
The following picture may help to understand what Helmut means
