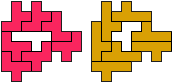
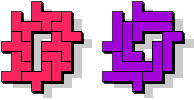
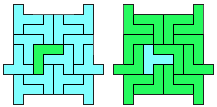
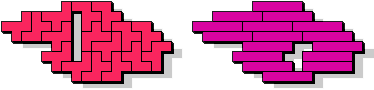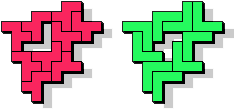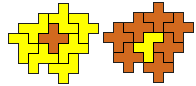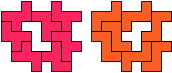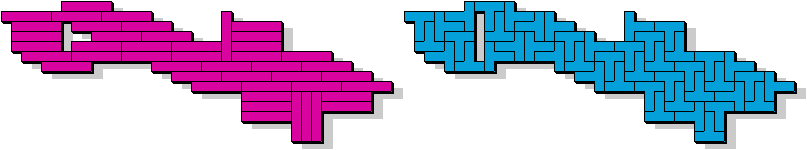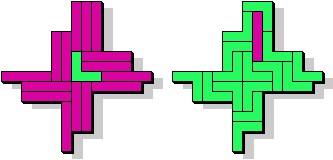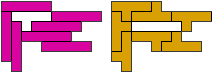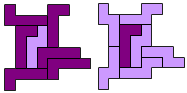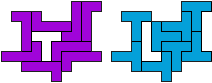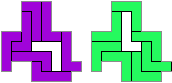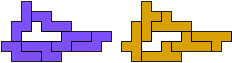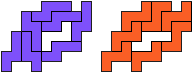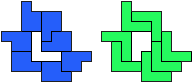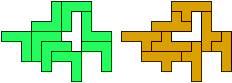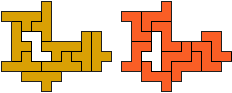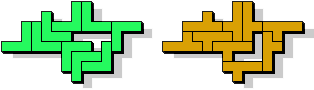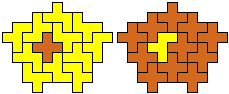Jenard Cabilao of the Philippines
Op 23 januari 2016 kregen we een mail van George Sicherman: "Congratulations on winning the 2012 GAPE Award! It is high time that your work with Yin-Yang Pentominoes was recognized publicly--not to mention the work of the other human and non-human contributors." Op 29 januari kregen we per post de trofee toegestuurd.
Kate verklaarde de lange wachttijd: " Our presentation of the 2012 GAPE Award was much delayed by our desire to design a unique prize for an international team of 8 puzzlists for their Yin-Yang Pentominoes project. Finally we found the right results"
Het was het wachten waard!

We zochten het aantal oplossingen met FlatPoly (de hexomino's zijn eenzijdig want daar staan de namen op)
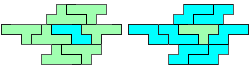
In 2019 ontmoeten we Helmut Postl op de bridges-conferentie in Linz. We gaven hem de trofee want Helmut heeft de mooiste bijdrage geleverd.
We kregen van Helmut een verhaal over de manier waarop hij een oplossing zelf had gevonden.
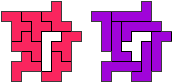
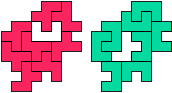
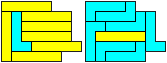
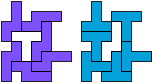
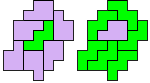
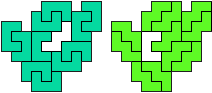
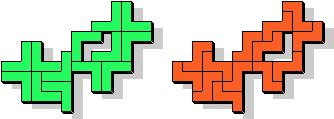
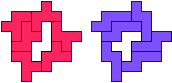
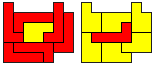
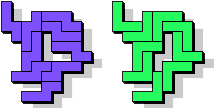
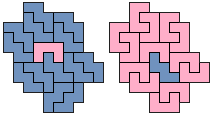
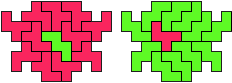
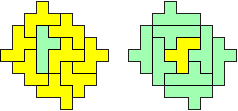
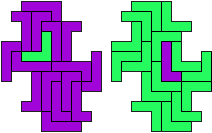
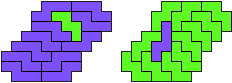
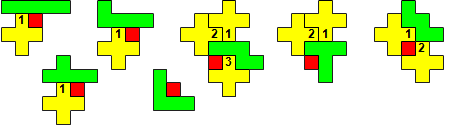
"Well, the first part was the left half. I found it nice to have the green W in the left upper „corner“. It looked to me as if the sunlight is reflected there.
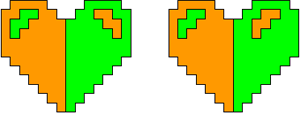
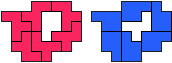
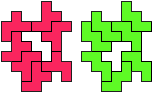
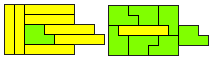
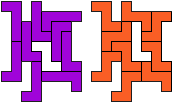
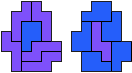
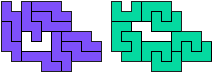
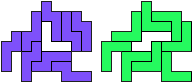
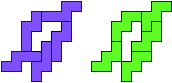
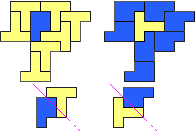
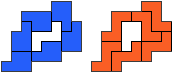
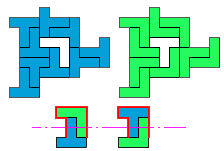
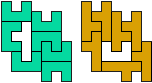
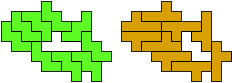
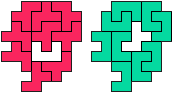
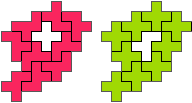
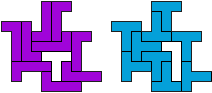
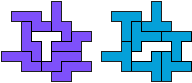
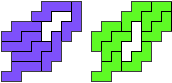
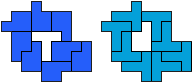
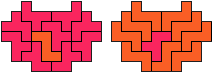
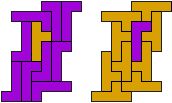
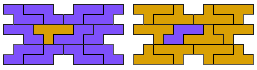
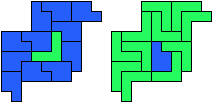
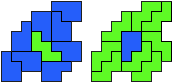
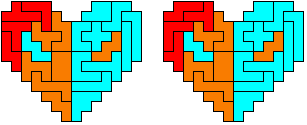
So I thought that it would be nice to have a symmetric pattern. But I did not find a solution for the right half. Then I changed the orange W to be at the same side as the green W so as the sunlight is reflected there in the same way. But I still did not find a solution. Then I tried various places for the orange W, and finally I came up with the solution in the third drawing. There is another solution close to it which arises when the Y-pentomino and the 2x3-hexomino change place (fourth drawing).
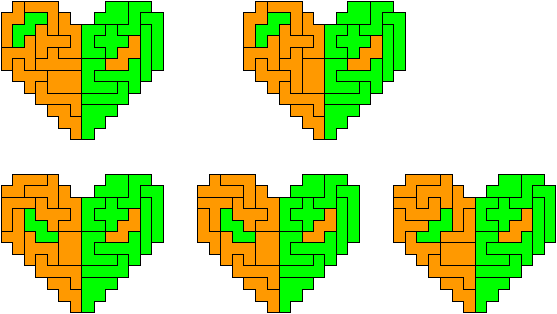
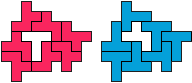
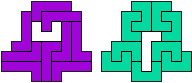
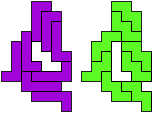
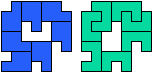
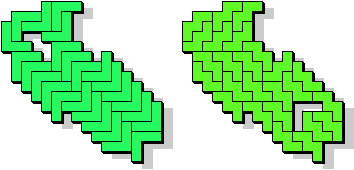
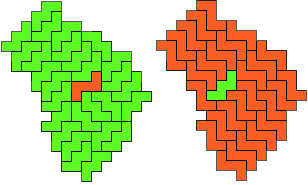
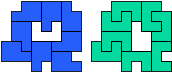
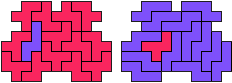
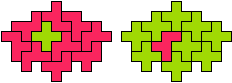
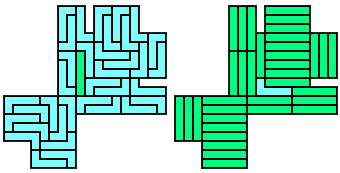
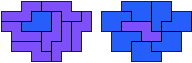
So well, this solution did not satisfy me all too much because it is not symmetrical. At this point, I let the computer run. And it found the following results: The right part is unique, and the left part has five solutions where I found two of them. The next two are indeed symmetrical. And furthermore - what I have ignored so far - the names on the pieces are written in the correct way. In my solution, one piece is flipped over, so this name lies on the bottom and is to be read with a mirror. I should have looked at this from the beginning. Then it may have been easier since the number of arrangements is smaller. Well...
But nevertheless it would have been nice if the solutions had been unique."
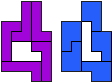
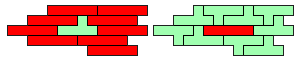
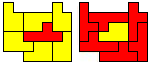
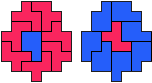
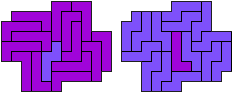
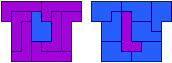
George Sicherman:"Jenard Cabilao of the Philippines has sent me a new pentomino problem, which I call 'Yin/Yang Pentominoes.'
Here is one example."
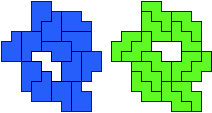
PW - 14 pentomino's (GS)
George: "With P/W, you can see how I do it!"
Helmut Postl stuurde ons een document :"Here is my method of constructing Yin/Yang patterns. Well, it looks so simple that it seems possible to find a lot of solutions there. So it is a nice condition to minimize the area of the pattern."
Choose two pentominoes. Look for a (small) shape which can be tiled by each pentomino.
For example, take P and W. They both tile the following shape (not unique, of course):
Next, stick both pentominoes together in a rather arbitrary way, for example:
Finally, arrange several copies of the first shape around this „center“ part. Preferably, there should be no holes left, and the center part should be completely surrounded. For example:
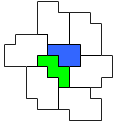
Now we are already done. Tile the shape copies as indicated in both ways. This is exactly George’s pattern on the site (zie bovenaan).
Remark: This method is not restricted to pentominoes. One can use two arbitrary polyominoes of same size where there exists a shape that can be tiled by each of the two polyominoes. The center part may not even be connected. It only must be possible to surround it. The method is not even restricted to polyominoes of same size. The only condition is the existence of a shape which can be tiled by both polyominoes.
An example for the latter is the following:
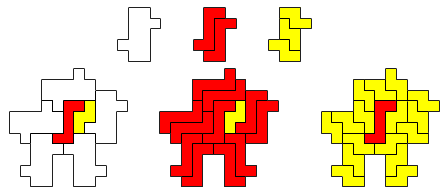
George: "With some pairs of pentominoes it is not so easy. The smallest holeless compatibility figure for T and W has 16 tiles!
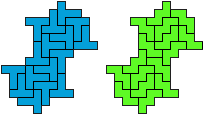
My other 'method' for yin/yang is brute force. I have a program that finds all ways to surround a polyomino with copies of another.
I check them all to see whether they can also be tiled with copies of the first polyomino around the second.
If that does not work, I have another program that adjoins a polyomino to another in all possible ways ..."
Helmut Postl vroeg: "Is there any restriction to the Yin/Yang patterns? Number of pieces per pattern? Shape of the pattern? Orientation of the pieces? If not, there will be infinities of solutions.
One can try to approximate the Yin/Yang shapes, for example.
George: "The two figures must have the same shape, except for their holes. This is a severe restriction!"
De mooiste oplossing kregen we van Helmut Postl. Schitterend !!!

Hier is nog een voorbeeld van Livio Zucca
"I think LZ should be of Livio Zucca by law!"
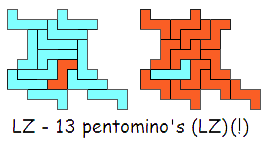
We plaatsen alleen de oplossingen van elke combinatie met het minst aantal pentomino's.
We kregen er van George Sicherman (GS), Aad van de Wetering (AW) , Aad Thoen (AT) , Helmut Postl (HP), Livio Zucca (LZ), Green Man (GM) en Odette De Meulemeester(OM)
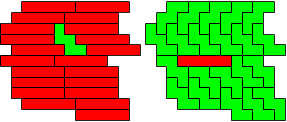
Op 01-01-2014 kregen we van George de volgende mail: "The world of Yin/Yang Pentominoes still visits mine from time to time, which is how I found this improved solution for the I and V pentominoes. It supersedes the "Green Man" solution as well as Helmut Postl's. (I hope the Green Man will not blow *another*gasket!) "
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
George: "Gat is gat! I prefer 'clean' holes, but not when they cost extra
tiles."
Wij vinden puntcontacten niet mooi daarom staan hieronder oplossingen zonder
puntcontacten.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Op 5 juli 2022 verbeterde George zijn eigen record van NV
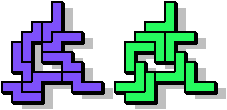
|
Thirty spokes share the wheel's hub; |
Tao Te Ching - Lao Tzu - hoofdstuk 11 |
Op aanvraag van George
Sicherman openen we een nieuwe tabel met symmetrische vormen.
"I like symmetry because it is symmetrical!"
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Van George Sicherman kregen
we een totale symmetrie: "Eén, twee, drie ,vier ..."
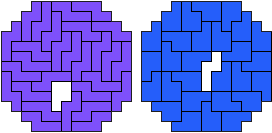
Om Livio's idee van symmetrie
gemakkelijk te kunnen toepassen kregen we van George Sicherman een
overzicht met de combinaties waarop we het idee kunnen toepassen
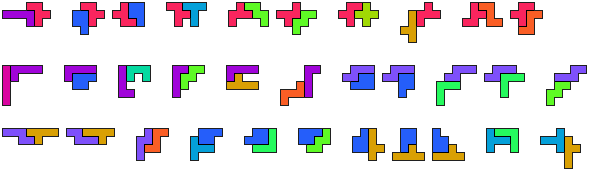
Je kan alles ook vinden op onze site bij
symmetrie
Onze groene man is terug van
zijn planeet
|
|
Livio Zucca:"My Green Friend sent me three solutions
'of his own'.
Wij vinden puntcontacten niet mooi daarom staan hieronder oplossingen zonder
puntcontacten.
Dubbele omsluitingen: (idee van Aad
Thoen)
We kregen ook nog een tripel van Aad
Thoen. Santé
George Sicherman: "Here is a rectangular triple!"
We kregen van George ook een quintuplet
En inderdaad! Onderstaande
oplossing kregen we van Livio Zucca
He says:
"I do not understand why
impose restrictions if they are not in the rules. This, to us, is called 'moralism'.
Or is it 'aesthetic'? If so, my solutions seem fine to me".
Oh ... :-) I will not argue philosophically if he is right or not, I have to
accept him for what he is. Publish it or not, as you wish."
Natuurlijk gaan we dit publiceren, maar George Sicherman: "If we
allow holes, we can do better than Mr. Green! I prefer to beat Green Man.
When I beat Helmut, he beats back!"
GM says: "It was just to warm up the engine". : -]
(note the emoticon with the square mouth)
We kregen van Groene Man een oplossing voor PX van 17 maar met een gat bij
de omrande X-pentomino. Toen we hem mailden dat we dat eigenlijk niet wilden
mailde hij: "Very interesting. Another way on planet Earth, for the
spontaneous formation of new ethical rules! [:-)]". Hij paste zich aan
en stuurde een oplossing van 18.
[GM] [:-)] : "Is it ethical if ...?
- There are holes
- The number of the pentominoes is less that the best solution without holes
- The single piece does not touch the perimeter or holes
- It is published on a separate list
I think yes."
We volgen hem.
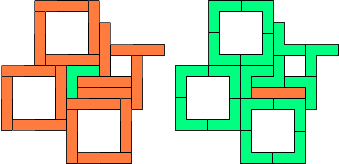
IV - 18 pentomino's (GM)
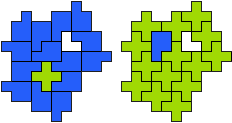
PX - 15 pentomino's (GS)
"It's not easy being green."
-Kermit the Frog
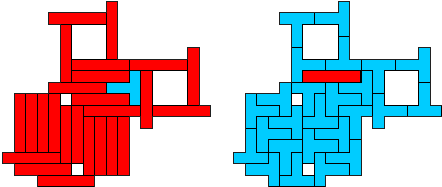
IT- 26 pentomino's (HP)
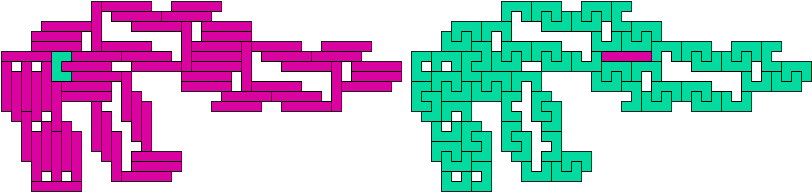
IU - 64 pentomino's (GS)
"I hope that Green Man will not blow a gasket!"

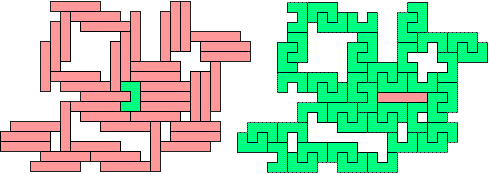
IU - 44 pentomino's
Here's a bit of enthusiasm [:-)]
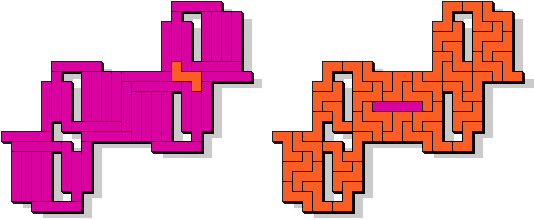
IZ - 42 pentomino's (GS)
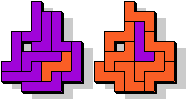
LZ - 9 pentomino's (GS)
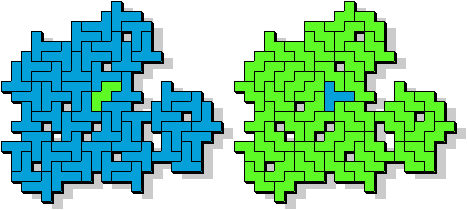
TW - 48 pentomino's (GS)
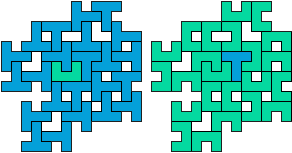
TU - 24 pentomino's (GS)

TY - 8 pentomino's (GS)
"Yellow + Blue = Green Man!"
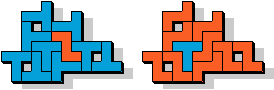
TZ - 10 pentomino's (GS)
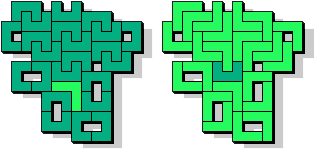
UV - 24 pentomino's (GS)
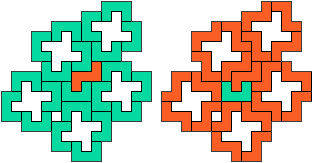
UZ - 22 pentomino's (GS)
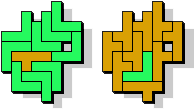
VY - 10 pentomino's (GS)
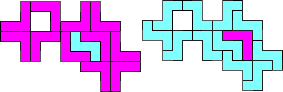
VZ - 12 pentomino's (GM)
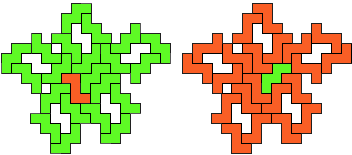
WZ - 22 pentomino's (GM)
Van
Helmut Postl kregen we het bewijs dat sommige combinaties namelijk
IX, LX, NX, PX, TX, UX, VX, WX, XY niet mogelijk zijn.
We want to surround the other pentomino (green) with copies of X (yellow).
Follow the numbers: First try to cover cell 1 with an X. Then do the
same with cell 2, and so on. The given sequences are unique (taking
the symmetry of the W into account) and result in a red cell which
cannot be covered anymore.
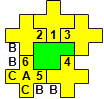
The impossibility of P and U is somewhat different. The above
construction for P does not directly yield a red cell. But we have
the following: None of the four B-cells can be covered by an X
without creating holes. For the same reason, none of the C-cells can
be connected to the rest of the pattern that is separated by the
A-cell. This part of the pattern contains the cells numbered 5 and 6
and a number of complete pentominoes – call it the „body“. Therefore,
the area of the body is congruent 2 mod 5. Now cover the whole
pattern with one X and copies of P. The A-cell belongs to the
perimeter (because of the empty B-cells) and therefore must be
covered by a P. In each case, the remaining area of the body is
either 2 or 3 mod 5 and can therefore not be completely covered by
polyominoes. Contradiction.
Finally, assume a possible pattern covered by U and X. Consider the
topmost grid line that touches some pentomino. Then each cell
touching this line must have at least two empty neighbor cells on
both sides in order to be covered by an X. But then, this cell
cannot be covered by a U without leaving all four neighbors empty.
![]()
George:"I do not think
that Jenard intended to limit the figures to rectangles!
This page shows which pairs of pentominoes are certainly impossible
for rectangles:
http://www2.stetson.edu/~efriedma/mathmagic/0810.html
I agree that rectangles are a good place to start!"
We plaatsen ook de combinaties binnen een rechthoek met het
minst aantal pentomino's
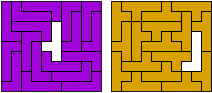
LY - 18 pentomino's (GS)
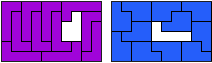
LP - 12 pentomino's (GS)
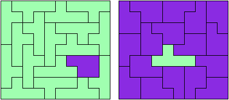
PY - 18 pentomino's
George Sicherman:"After all this HARD work, I decided to look for
something easier--tetrominoes! One is missing. You will easily see why."
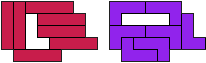
il - 8 tetromino's (GS)

in - 8 tetromino's (GS)
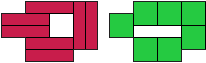
iq - 8 tetromino's (GS)

it - 8 tetromino's (GS)
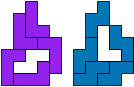
ln - 6 tetromino's (GS)
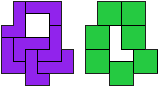
lq - 8 tetromino's (GS)
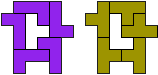
lt - 6 tetromino's (GS)
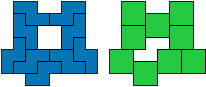
nq - 10 tetromino's (GS)
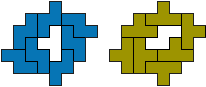
nt - 8 tetromino's (GS)
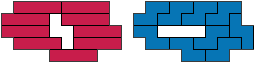
in - 10 tetromino's (GS)
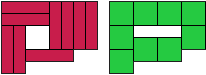
iq - 10 tetromino's (GS)
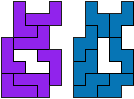
ln - 8 tetromino's (GS)
Soms wordt er gebruikt gemaakt van de methode van Helmut Postl (zie
hierboven)
Je kan misschien een begin vinden op onze pagina's
http://www.pentomino.classy.be/congdeco4.html
http://www.pentomino.classy.be/congdeco5.html
http://www.pentomino.classy.be/congdeco6.html
George maakte van de meeste oplossingen brandhout!
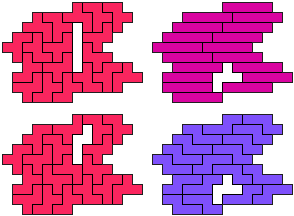
FI-FN - 19 pentomino's (GS)
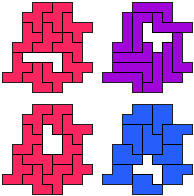
FL-FP (Flip-Flop) - 11 pentomino's (GS)
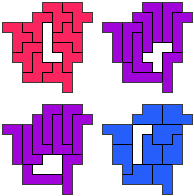
FL-LP - 10 pentomino's (GS)
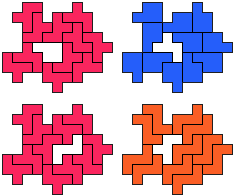
FP-FZ - 12 pentomino's (GS)
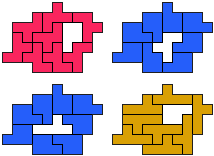
FP-PY - 9 pentomino's (GS)
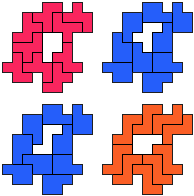
FP-PZ - 10 pentomino's (GS)
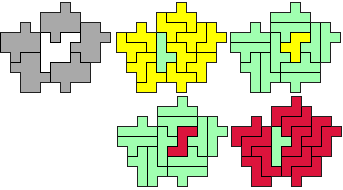
FY-YZ - 12 pentomino's (OM)
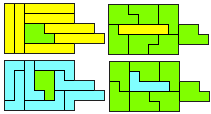
IP-LP - 8 pentomino's (AT)
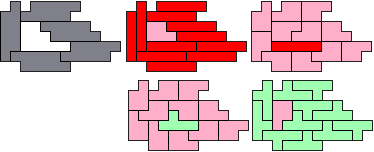
IP-PY - 12 pentomino's (OM)
GS heeft een triple met 9 zie verder.
Eigenlijk moet het weg maar het is mooi toch?
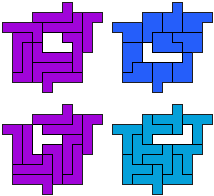
LP-LT - 11 pentomino's (GS)
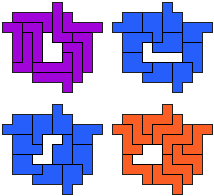
LP-PZ - 11 pentomino's (GS)
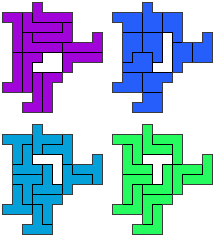
LP-TV - 12 pentomino's (GS)
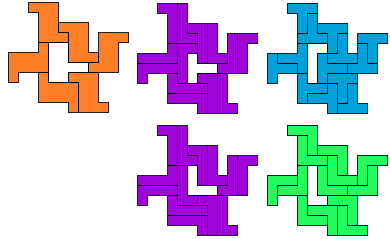
LT-LV - 14 pentomino's (GS)
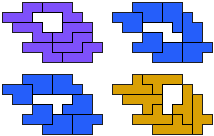
NP-PY - 8 pentomino's (GS)
George Sicherman vulde onze kelder goed aan.

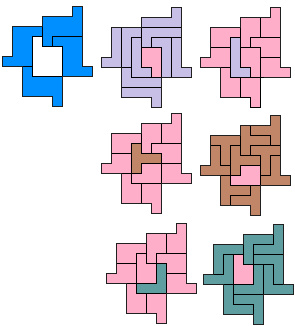
LP-PT-PV - 9 pentomino's (AT)
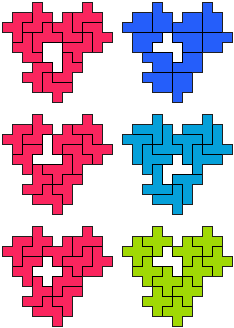
FP-FT-FX - 12 pento's (GS)
De vorm lijkt wel een hart!
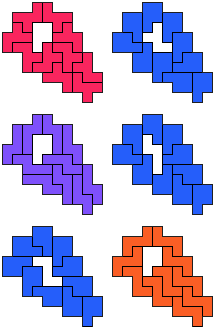
FP-NP-PZ - 11 pento's (GS)
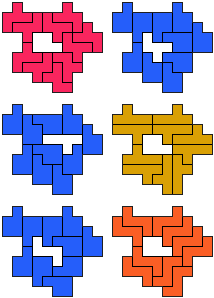
FP-PY-PZ - 11 pento's
(GS)
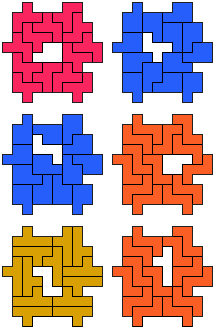
FP-PZ-YZ - 14 pento's (GS)
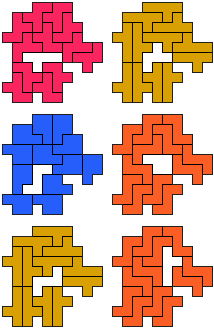
FP-PZ-YZ - 13 pento's
(GS)
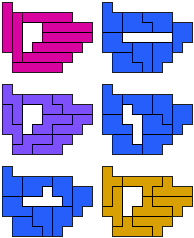
IP-NP-PY - 9 pento's (GS)

IY-LP-LY - 12 pento's (GS)
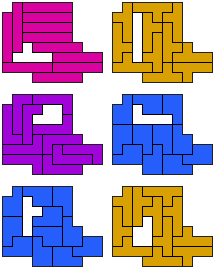
IY-LP-PY - 12 pento's
(GS)
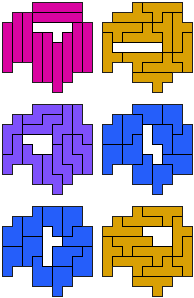
IY-NP-PY - 12 pento's
(GS)
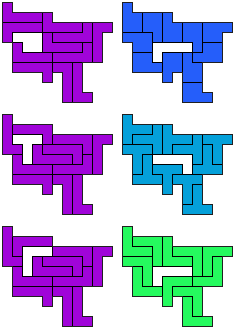
LP-LT-LV - 12 pento's
(GS)

LP-LY-PY - 18 pentomino's (GS)
George vond ook nog 3 quadruplets
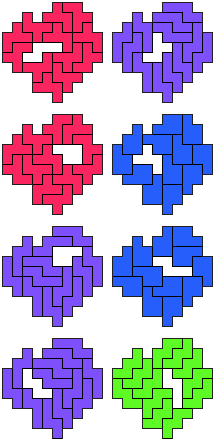
FN-FP-NP-NW-13 pento's (GS)
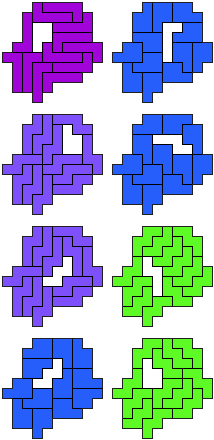
LP-NP-NW-PW-13 pento's (GS)
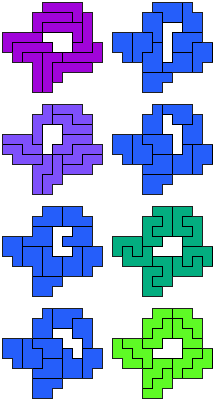
LP-NP-PU-PW-11 pento's (GS)

FN-FP-FW-NP-NW - 14 pentomino's (GS)
Het kon nog beter: George Sicherman vond een sextuple !
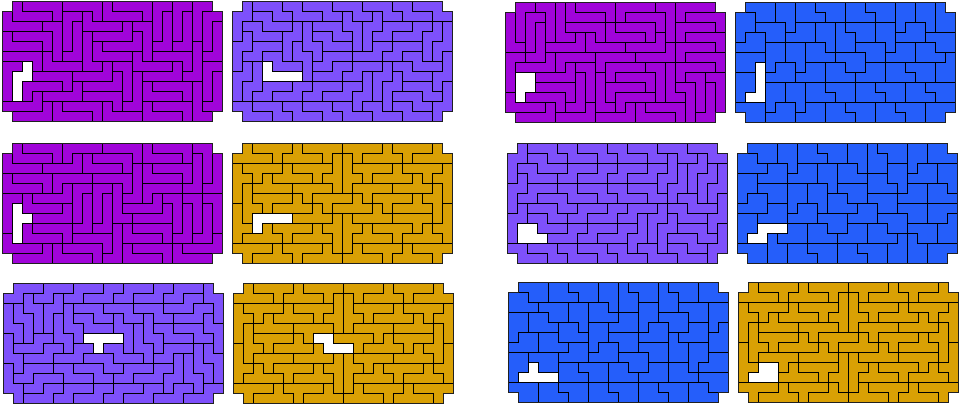
Maar Helmut is de beste: een 10-tuple
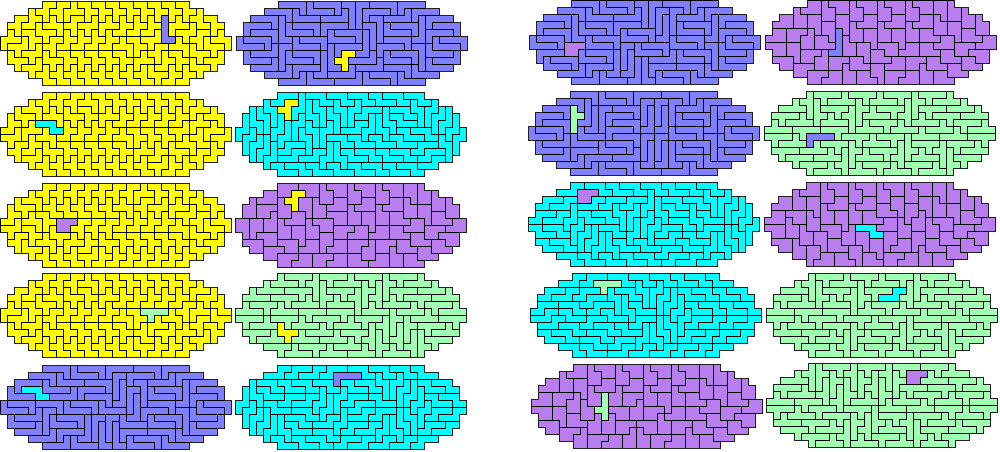
Maar Helmut kon nog beter: een 15-tuple

George:"My figures have a hole, so extra holes are odious. And Aad
Thoen's solution for IN falls apart!"
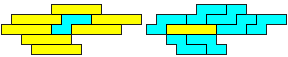
"I think that there are no other Double Dutch pairs--but I never know what
will happen when a certain Italian takes a hand!"
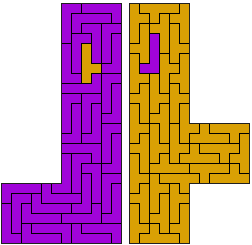
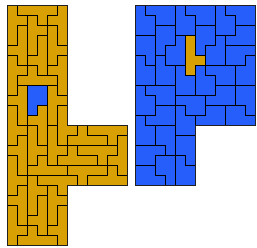
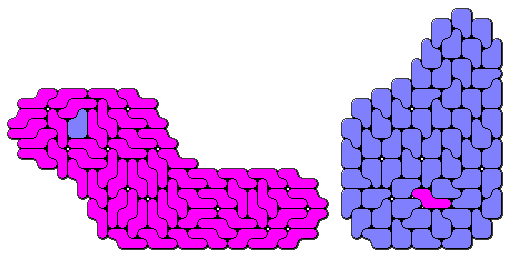
Leonardo Da Vinci said: "If a piece does not enter we can round it!"
We eindigen met dit plaatje omdat we het mooi vinden. (gekregen van Livio
Zucca)
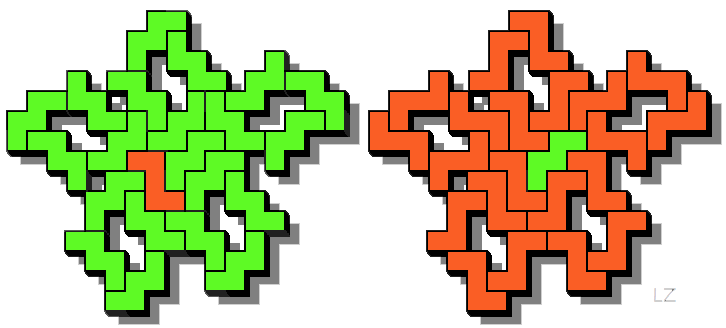
We zijn er van overtuigd dat er veel meer oplossingen te vinden zijn (al dan
niet in een rechthoek - liefst met zo weinig mogelijk pentomino's)
Oplossing gevonden?
![]()
![]()