Pentomino's in een vierkant leggen
Martin Watson publiceerde op
Nobnet de FFFFFFFFFFF-puzzle which stands for FAIRLY FESTIVE FROSTY FUN, FREQUENTLY FURTIVE FABULOUS
FROLIC FOR FAVOURITE FUNSTERS.
Bob Henderson vestigde onze aandacht op deze pentomino-puzzel. Bedankt Bob!
Leg 11 F-pentomino’s op het witte geruite vierkant (8 op 8) . Vierkantjes moeten
precies op vierkantjes vallen en de pentomino’s mogen elkaar niet overlappen. (Er is juist 1 oplossing.)
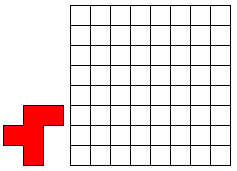
Wil je ons exelbestandje om gemakkelijk te zoeken?
11 F-PENTOMINO'S
Oplossing
We maakten analoge opgaven voor de andere pentomino's.
Leg 12 I-pentomino’s op het witte geruite vierkant (8 op 8) . Vierkantjes moeten
precies op vierkantjes vallen en de pentomino’s mogen elkaar niet overlappen. (Er is juist 1 oplossing.)
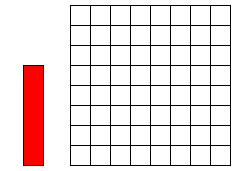
Wil je ons exelbestandje om gemakkelijk te zoeken?
12 I-PENTOMINO'S
Oplossing
Leg 12 L-pentomino’s op het witte geruite vierkant (8 op 8) Het zwarte vierkant (2 op 2) in het midden blijft leeg. Vierkantjes moeten
precies op vierkantjes vallen en de pentomino’s mogen elkaar niet overlappen. (Er is juist 1 oplossing.)
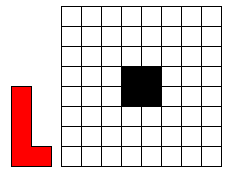
Wil je ons exelbestandje om gemakkelijk te zoeken?
12 L-PENTOMINO'S
Oplossing
Leg 12 N-pentomino’s op het witte geruite vierkant (8 op 8) . Vierkantjes moeten
precies op vierkantjes vallen en de pentomino’s mogen elkaar niet overlappen. (Er is juist 1 oplossing.)
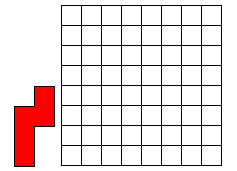
Wil je ons exelbestandje om gemakkelijk te zoeken?
12 N-PENTOMINO'S
Oplossing
Leg 12 P-pentomino’s op het witte geruite vierkant (8 op 8) .In het eerste geval moeten de hoeken vrij blijven en in het tweede geval blijft het zwarte vierkant in het midden leeg. Vierkantjes moeten
precies op vierkantjes vallen en de pentomino’s mogen elkaar niet overlappen. (Er is telkens juist 1 oplossing.)
Wil je ons exelbestandje om gemakkelijk te zoeken?
12 P-PENTOMINO'S
Oplossing
Leg 10 T-pentomino’s op het witte geruite vierkant (8 op 8). De hoeken moeten leeg blijven. Vierkantjes moeten
precies op vierkantjes vallen en de pentomino’s mogen elkaar niet overlappen. (Er is juist 1 oplossing.)
Wil je ons exelbestandje om gemakkelijk te zoeken?
10 T-PENTOMINO'S
Oplossing
Leg 11 U-pentomino’s op het witte geruite vierkant (8 op 8). De hoeken moeten leeg blijven. Vierkantjes moeten
precies op vierkantjes vallen en de pentomino’s mogen elkaar niet overlappen. (Er zijn 12 oplossingen.)
Wil je ons exelbestandje om gemakkelijk te zoeken?
11 U-PENTOMINO'S
Oplossing
Leg 12 V-pentomino’s op het witte geruite vierkant (8 op 8) . Vierkantjes moeten
precies op vierkantjes vallen en de pentomino’s mogen elkaar niet overlappen. (Er is juist 1 prachtige oplossing: de figuur heeft een symmetriemiddelpunt.)
Wil je ons exelbestandje om gemakkelijk te zoeken?
12 V-PENTOMINO'S
Oplossing
Leg 12 W-pentomino’s op het witte geruite vierkant (8 op 8) . Vierkantjes moeten
precies op vierkantjes vallen en de pentomino’s mogen elkaar niet overlappen. (Er is juist 1 oplossing.)
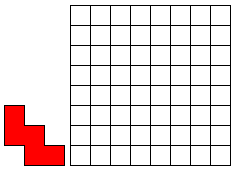
Wil je ons exelbestandje om gemakkelijk te zoeken?
12 W-PENTOMINO'S
Oplossing
Leg 8 X-pentomino’s en 4 Y-pentomino's op het witte geruite vierkant (8 op 8) . Vierkantjes moeten
precies op vierkantjes vallen en de pentomino’s mogen elkaar niet overlappen. (Er is juist 1 prachtige oplossing: de figuur heeft een symmetriemiddelpunt.)
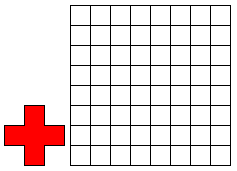
Wil je ons exelbestandje om gemakkelijk te zoeken?
8 X-PENTOMINO'S
Oplossing
Er is nog juist 1 legging met 8 X-pentomino's die ook een symmetriemiddelpunt bezit. Kan je die vinden?
Oplossing
Leg 12 Y-pentomino’s op het witte geruite vierkant (8 op 8). De hoeken moeten leeg blijven. Vierkantjes moeten
precies op vierkantjes vallen en de pentomino’s mogen elkaar niet overlappen. (Er is juist 1 oplossing.)
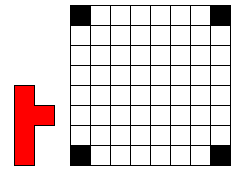
Wil je ons exelbestandje om gemakkelijk te zoeken?
12 Y-PENTOMINO'S
Oplossing
Leg 10 Z-pentomino’s en 2 V-pentomino's op het witte geruite vierkant (8 op 8) . Vierkantjes moeten
precies op vierkantjes vallen en de pentomino’s mogen elkaar niet overlappen. Er zijn 2 oplossingen.
De ene oplossing heeft een symmetriemiddelpunt en bij de andere oplossing heeft de figuur die bestaat uit de Z-pentomino's een verticale symmetrieas.
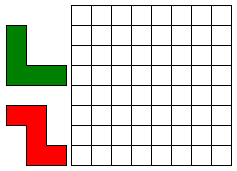
Wil je ons exelbestandje om gemakkelijk te zoeken?
10 Z-PENTOMINO'S
Oplossing
Aad van de Wetering had de volgende commentaar bij deze opgave:"Er zitten heel fraaie oplossingen bij, wonderlijk! Ik heb ook nog even de 11 F-pento's in een ruimte van 4x4x4 gestopt, ook dan is er maar een oplossing mogelijk. Maar die is niet echt fraai. Wel fraai natuurlijk dat ie uniek is."











