Pento-Sudoku
In het wiskundetijdschrift
Pythagoras van november 2005 stond het artikel "SUDOKU light"
Vraag 4 kwam ons heel bekend voor. Hadden ze hun inspiratie op onze site
gezocht? Dit leek ons
potpourri-probleem 1.
Naar aanleiding hiervan maakten we met zijn allen
een pento-sudoku.
Hier volgen alle opgaven.
Vul de getallen 1, 2, 3, 4 of 5 in zodat deze per rij, per kolom en op elke
pentomino juist 1x voorkomen.
Voor de oplossing kan je telkens op de opgave
klikken.
Onze oplossingen konden we heel makkelijk maken dank zij de praktische
Clics-blokken.
Met heel veel dank aan Aad van de Wetering die
ons hielp bij het bepalen van een opgave met zo weinig mogelijk
startcijfers.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In het
Sint
Willibrordcollege te Goes was de eerste vraag van de
weekendpuzzel 16 in de ladderwedstrijd een pentominosudoku.
We kregen hem toegestuurd van Floor van Lamoen. Bedankt!
Het Sint Willibrordcollege is gefuseerd. De nieuwe school heet
ostrealyceum.
Ook deze maakte Aad met 4 startcijfers
|
|
|
Je kan ook pento-sudoku's on
line spelen op
de SUDOKUkids-site
Tijdens de lessen Elektriciteit maakten we een
lampjes-pento-sudoku. Hij is echt
heel mooi als kerstversiering.
We weten van geen ophouden. We hebben een sudoku
gemaakt met hetzelfde cijfer op de diagonaal.
Nog meer voorbeelden zijn te vinden op de site
van
Bob Harris.
Wil je de oplossing zien, klik dan op de opgave (eerst
zelf zoeken!)
Wil je de oplossing zien, klik dan op de opgave (eerst
zelf zoeken!)
Wil je een niet-gekleurde opgave om in zwart-wit af te drukken, druk dan
hier boven op de opgave. Goede oplossers verwerven eeuwige roem. Op de site van
Natuur,wetenschap en techniek is er
maandelijks een prijsvraag. De
prijsvraag van het novembernummer 2008 was
een wormsudoku. Voor een wormsudoku gelden de
klassieke regels (in elke kolom, elke rij en elk hokje van 3 bij 3 de
getallen 1 t/m 9), plus dat in elke worm de getallen oplopend zijn van de
staart naar de ogen. In sommige wormen zijn de ogen ingetekend, in andere
nog niet. Van Aad van de Wetering kregen
we in februari 2020 nog twee pento-sudoku's.
Ter gelegenheid van feestdagen kreeg onze pento-sudoku een ander uitzicht.
Je kan op de onderstaande foto's klikken.
Kerstmis
Valentijn
Tijdens de lessen hout werden
dobbelstenen gemaakt voor onze sudoku.
Zelfs zonder I en P pento te gebruiken kunnen we
nog heel veel verschillende sudokus maken. We vroegen ons af of we ook
pento-udokus konden maken (ook op de diagonalen de cijfers van 1 tot 5).
Van Helmut Postl kregen we het volgende antwoord:"no, there is indeed no
Udokus with 5 different pentominoes, no P and no I, so that both diagonals
are also fulfilled."
We kregen echter de volgende opgave
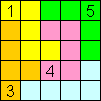
Dit is zelfs geen sudoku want hij heeft 6 verschillende
oplossingen.
Hij stelde echter als bijkomende voorwaarde dat
op 1 diagonaal de cijfers verschillend moeten zijn.
Kan je hem
oplossen?
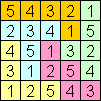
Er is nog één
pentominoveld dat hiervoor kan dienen. kan je het vinden?
Een leuke variatie is de killer-pento-sudoku.
Vul de getallen 1, 2, 3, 4 of 5 in zodat deze per rij, per kolom en op elke
pentomino juist 1x voorkomen.
Het getal dat aan de stippellijn staat is de som van de getallen die in de
aangestippelde vakjes staan.
Je kan ook
killer-sudoku on line spelen.
Op
http://www.mathpuzzle.com/ bij het
materiaal bijgevoegd op 7 september 2008 vonden we de KenKen puzzel.
Meer voorbeelden kan je vinden op
http://www.kenken.com/
We vroegen Aad van de Wetering of hij zoiets kon maken op een
pentominoveld en hieronder zie je de opgave:
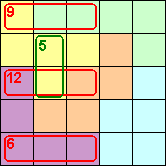
Eigenlijk vonden we dit een killer-pento-sudoku
Wil je de oplossing zien, klik dan op de opgave (eerst
zelf zoeken!)
Toen we aan Bob Harris onze pagina mailden was zijn antwoord:"They look interesting. I will try them soon if I get some time. I am
currently doing a lot of work involving Orangutan DNA alignments. Andrew
Clarke has created some similar ones, I think.
I also have some overlapping sudokus, see this page:
Zijn overlapping sudokus zijn wel erg leuk!
We gingen op de uitgebreide
PolyPages van Andrew op zoek en vonden er heel wat
varianten
http://www.recmath.com/PolyPages/PolyPages/index.htm?PolySudoku.html maar
de pentoku van Aad vinden we de beste ;-)
We maakten ook nog kleiner
dan-killer-pento-sudoku's.
Op 14 oktober 2008 publiceerde Aad van de Wetering op
Jaspers Cryptogrammen Site een
X-pentoku.
We vonden dit een schitterend idee maar ook heel leuk om op te lossen. We
vroegen aan Aad of hij voor ons nog enkele andere opgaven wou maken en
verder zie je zijn antwoord. Hij maakte ze allemaal.
Heel veel dank!
Vijf 5x5 sudoku's vormen samen een grote pentomino, gebruik de
cijfers 1 t/m 5 om ze te vullen. De pentomino's bevatten ook de cijfers 1
t/m 5, ze zijn soms grensoverschrijdend.
Er zijn 11 startcijfers.
Er zijn 12 startcijfers.
Er zijn 11 startcijfers.
Er zijn 13 startcijfers.
Er zijn 12 startcijfers.
Er zijn 12 startcijfers.
Er zijn 11 startcijfers.
Er zijn 11 startcijfers.
Er zijn 14 startcijfers.
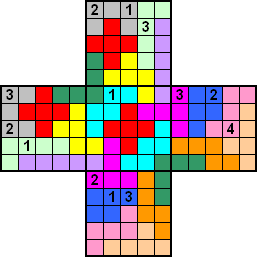
Er zijn 13 startcijfers.
Let ook eens op de symmetrie-as
van de vulling van de pentomino's!
Er zijn 11 startcijfers.
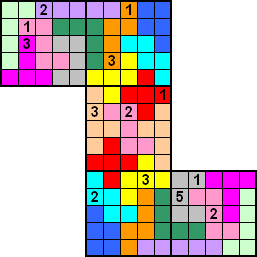
Er zijn 13 startcijfers.
Let ook eens op de mooie symmetrie
van de vulling van de pentomino's!
Wil je graag de oplossingen in exel om op te lossen druk dan hieronder:
F-pentoku
I-pentoku
L-pentoku
N-pentoku
P-pentoku
T-pentoku
U-pentoku
V-pentoku
W-pentoku
X-pentoku
Y-pentoku
Z-pentoku
Na de mooie symmetrie van de X en Z gingen we op zoek naar nog andere
symmetrische leggingen met 2 pentominosets + 1 pentoku op schaal 1/5.
We vonden dit nog voor de I-pentoku.
Vind je er nog andere dan horen we het graag.
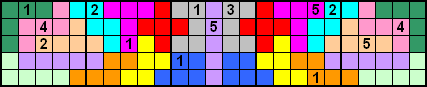
Er zijn 14 startcijfers.
Deze vulling vonden we ook nog speciaal. De rechthoeken van 5x12 zijn gevuld
met een pentominoset. Hiervoor bestaan 1010 verschillende oplossingen maar
slechts één waarbij de I-pento niet aan de rand komt.
Wil je een niet-gekleurde opgave om in zwart-wit af te drukken, druk dan
hier boven op de opgave.
Wil je graag de oplossingen in exel om op te lossen druk dan hieronder:
Symmetrische I-pentoku
Peter Jeuken voldeed aan onze oproep:" Ik kan een succesje melden met de
vondst van een symmetrische I-pentoku. Net als bij de Z-pentoku is er
symmetrie ten opzichte van het middelpunt. Bij deze oplossing komt geen
enkele van de drie I-pentomino's aan de rand."
We vroegen Aad of hij nog een pentoku wou maken en dat deed hij. Bedankt
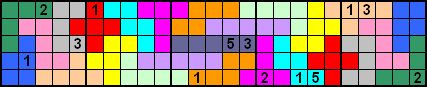
Er zijn 13 startcijfers
Wil je een niet-gekleurde opgave om in zwart-wit af te drukken, druk dan
hier boven op de opgave.
Wil je graag de oplossingen in exel om op te lossen druk dan hieronder:
Symmetrische I-pentoku
van Peter Jeuken
En Peter zocht maar verder:"Het is me gelukt om twee X-Sudoku-Pento's te
vinden met symmetriemiddelpunt. Als Aad opnieuw hier mooie startcijfers bij
bedenkt zal hij de puzzelaars (gezien de enthousiaste reacties) een groot
plezier doen."
We vroegen het aan Aad. De eerste had geen oplossingen, merkwaardig!
En de tweede:
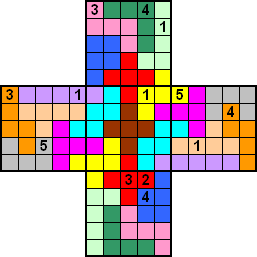
Er zijn 13 startcijfers
Wil je een niet-gekleurde opgave om in zwart-wit af te drukken, druk dan
hier boven op de opgave.
Wil je graag de oplossingen in exel om op te lossen druk dan hieronder:
Symmetrische X-pentoku
van Peter Jeuken
Mail naar:
OdetteDM@outlook.com
Naam
Land
Pentoku
Aad van de Wetering
Nederland
F-I-L-N-P-T-U-V-W-X-Y-Z
I met symmetrie-as
I met symmetriemiddelpunt
X met symmetriemiddelpunt
Odette De Meulemeester
België
F-I-L-N-P-T-U-V-W-X-Y-Z
I met symmetrie-as
I met symmetriemiddelpunt
X met symmetriemiddelpunt
Bert ten Hoeve
Nederland
F-I-L-N-P-T-U-V-W-X-Y-Z
I met symmetrie-as
I met symmetriemiddelpunt
X met symmetriemiddelpunt
Martin Friedeman
Nederland
F-I-L-N-P-T-U-V-W-X-Y-Z
I met symmetrie-as
I met symmetriemiddelpunt
X met symmetriemiddelpunt
Lisan Sanders
Nederland
F-I-L-N-P-T-U-V-W-X-Y-Z
I met symmetrie-as
I met symmetriemiddelpunt
X met symmetriemiddelpunt
Peter Jeuken
Nederland
I met symmetriemiddelpunt
X met symmetriemiddelpunt
Rien Verbeek
Nederland
F-I-L-N-P-T-U-V-W-X-Y-Z
I met symmetrie-as
I met symmetriemiddelpunt
X met symmetriemiddelpunt
Nico Looije
Nederland
F-I-L-N-P-T-U-V-W-X-Y-Z
I met symmetrie-as
I met symmetriemiddelpunt
X met symmetriemiddelpunt
Bert ten Hoeve:"ZEER VERSLAVEND. Ik liet
mijn koffie koud worden, en dat zegt wat ! Zeer veel dank, vooral ook aan
Aad ! Ik zie uit naar de volgende"
Op 22 oktober 2008 mailde Bert:"Waarom weet ik niet, maar tot nu toe
was de U het lastigst. Nu maar wachten op de rest ....
Hierbij de X die wel meeviel"
Wij vinden de L de meest lastige. Op
28 oktober beaamde Bert dit:"Inderdaad, die L is buitengewoon lastig,
veel moeilijker dan de U maar het blijft leuk werk".
Martin Friedeman:"Geweldig bedankt voor je mailtje, ik ga meteen
met de ‘F-Pentoku’ beginnen!"
Op 26 oktober 2008 kregen we van Martin opnieuw een mailtje:"Er gaat
niets boven het oplossen van een aantal ‘pentoki’ op een mistroostige,
herfstachtige zondagmiddag! Héérlijk! De oplossingen van een zevental
‘pentoki’ heb ik als bijlage toegevoegd; de oplossing van de ‘X-pentoku’
volgt spoedig."
"Ik vind de ‘L-pentoku’ tot nu toe ook de moeilijkste!"
Lisan Sanders:"De symmetrische I-pentoku
is gelukt, lijkt me. Erg leuk om te doen!! Nu weer verder met die twaalf
andere pentoku’s. Hartelijk bedankt voor dit moois."
"Ik wilde nog wel verder, maar helaas zijn ze op. Het lukte steeds beter,
behalve dan de L, maar die heb ik uiteindelijk ook klein gekregen. Heel erg
bedankt en je houdt me wel op de hoogte, hè, als je weer zoiets moois
ontwikkelt.Veel dank ook voor Aad."
Peter Jeuken:"Ik heb je aanbeveling om
het zonder computer op te lossen opgevolgd."
Rien Verbeek:"Als ik me niet vergist
heb, heb ik de oplossingen bijeengesprokkeld. Zoals ik al uit de commentaren
van collega-oplossers kon opmaken, was de L het moeilijkst!! Wat een
hersenkraker is dat!
Veel dank, ook aan Aad, voor dit smakelijke gerecht! Het was smullen
geblazen!
Naar aanleiding daarvan kregen we een mail van Aad van de Wetering:"Ook
wormen lusten pentokes"
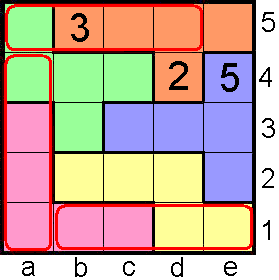
In het roodomrande moeten de cijfers ofwel alle oplopend ofwel alle
aflopend zijn.
Veel pier-plezier.
Wil je de oplossing zien, klik dan op de opgave.
Goede oplossers verwerven eeuwige roem.
Mail naar:
|
|
|
Ook beide diagonalen 1 t/m 9
In de pentomino's zijn alle cijfers
verschillend. Het centrale vakje is oneven.
De cijfers 4, 5 en 6 komen nooit meer dan een keer voor op een willekeurige
diagonaal.
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - België
Nico Looije - Nederland
Martin Friedeman - Nederland
Van Aad van de Wetering kregen
we in juli 2022 deze leuke opgave
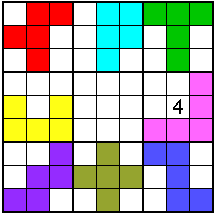
In de pentomino's is het verschil tussen orthogonale buren minstens 5.
Goede oplossers verwerven eeuwige roem.
Mail naar:
OdetteDM@outlook.com
Oplossers:
Aad van de Wetering - Nederland
Odette De Meulemeester - België
Martin Friedeman - Nederland
