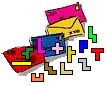
Since the surface of four pentominoes is 20, we must make a square with area 20.
We can get 20 as the sum of the squares of 2 and 4. So if we have a right triangle with sides 2 and 4 then the hypotenuse is the side of a square with area 20.
In pentominoes however, we find no right triangles with sides 2 and 4.
Therefore we simplify the square root:
The drawing below is from our syllabus of NWD 2002. Aad van de Wetering used 8 pieces to made from a 'PINT' a square.
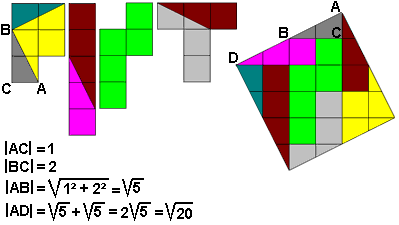
Katrijn Cierkens made from 'zuil' a square in 10 pieces. (zuil = Dutch for pillar)
We can do it in 9 pieces.
Can you do that?
Solution
We also have a geogebra animation
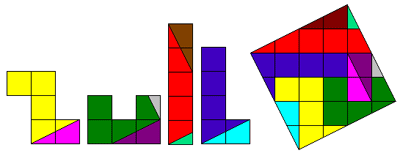
We can dissect 'tulp' in 8 pieces.(Thanks to Aad; tulp = Dutch for tulip)
We can dissect 'tuil' in 9 pieces. (TUIL = Dutch for bouquet)
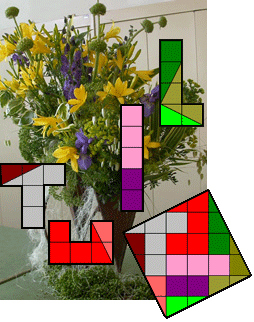
We can do it in 8 pieces.
Can you do that?
Solution
We also have a geogebra animation.
We have made with geogebra an
animation of
4
F-pentominoes
to a square,
4
I-pentominonoes to a square,
4 P-pentominoes to a square and
4 W-pentominoes to a square.
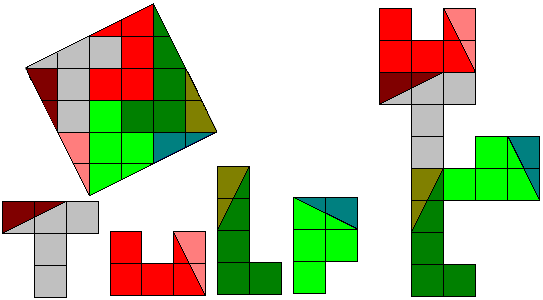
At our request Aad van de Wetering made of 'TUTU' a square in eight pieces. The
figure in the square has a symmetry center. Beautiful!
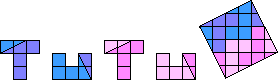
geogebra animation
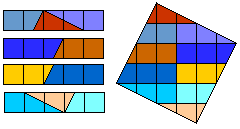
Helmut Postl dissected every four equal pentominoes to a square.
These are the minimum number of pieces:
F:8, I:10, L:8, N:8, P:8, T:9, U:10, V:8, W:10, X:9, Y:8, Z:8.
Especially the X in 9 pieces is well done!
If you do not hold color for printing, you can press the picture and then you
get the drawings without squares.
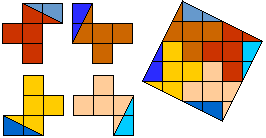 |
 |
 |
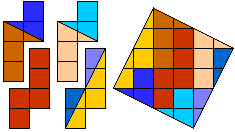 |
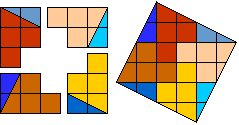 |
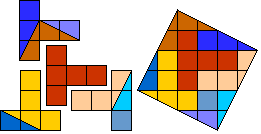 |
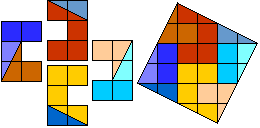 |
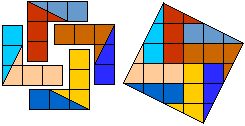 |
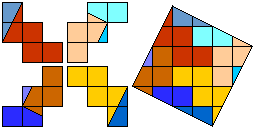 |
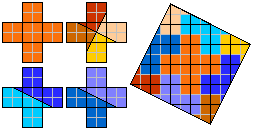 |
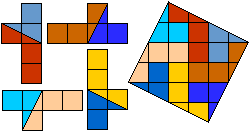 |
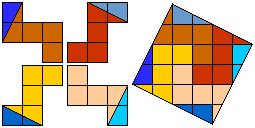 |
Comments mail to
o.d.m@fulladsl.be