We recieved this problem of Bob Henderson (USA) .

Use a set of tetrominoes to make a fence of the corner.

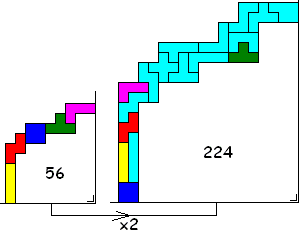
Make another fence with the same shape but twice as large in each dimension with the 5 tetrominoes and the 12 pentominoes.

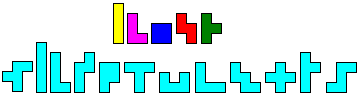
All polyominoes must be in one plane, polyominoes have to touch with at least one full side (just corner connection is illegal).
The enclosed area under the fence must be one enclosed area.
There’s a extra rule: the tetrominoes must lie in the same orientation as in the original pattern. (This is a idea of Helmut Postl.)

The main goal is to maximize the enclosed area.

In this example, the tetromino-fence has an enclosed area of 56

Do you have our excel file to draw the cornerfence? You can download it here.

'FlatPoly2', a programm by Aad van de Wetering, can be of great assistance when trying to find a solution. It can be downloaded at his site .