Voor de vergroting (260 = 65 x 4 ingesloten vierkantjes) zijn er 2 oplossingen.
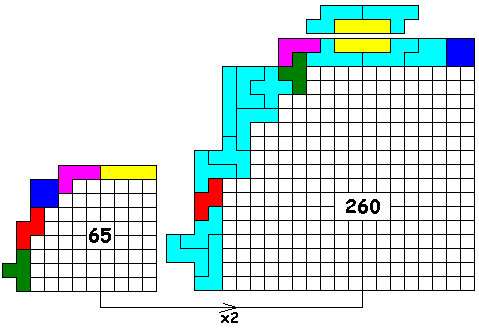
We kregen een maximum oplossing van:
| Bob Allen | USA |
| Gabriele Carelli | ItaliŽ |
| Peter en Ina Esser | Duitsland |
| Nisrine El Ahmadi | BelgiŽ |
| Patricia Etcheverry | ArgentiniŽ |
| GaŽl Gaytant | BelgiŽ |
| Christian Gillen | Luxembourg |
| Bob Henderson | USA |
| Roel Huisman | Nederland |
| Tom Jolly | USA |
| Kate Jones en Michael Keller | USA |
| Sammy Khiter | BelgiŽ |
| Jan Kok | Nederland |
| Jochim Liveyns | BelgiŽ |
| Andres Olmos | Colombia |
| Stefano Popovski | Bulgarije |
| Helmut Postl | Oostenrijk |
| Vivien Schiettecatte | BelgiŽ |
| Timoty Snauwaert | BelgiŽ |
| Sergio Stanzani | ItaliŽ |
| Pieter Torbijn | Nederland |
| Dario Uri | ItaliŽ |
| Berend Jan van der Zwaag | Nederland |
| Aad van de Wetering | Nederland |
| Ken Vanherpen | BelgiŽ |
| Arťlien Vanhoubroeck | BelgiŽ |
| Miguel Vanlierde | BelgiŽ |
| Johan Viljoen | Zuid Afrika |
| ItaliŽ |
Op 10 januari 2003 mailde Gabriele Carelli ons dat hij nog een tweede oplossing van 65 gevonden had door de I- en T-tetromino van plaats te wisselen, maar dat deze geen vergrote oplossing heeft.

Op 24 februari 2003 bevestigde Berend Jan van der Zwaag dit.
Berend Jan mailde:"Ik vond nog een andere tetrominohoekinsluiting met een ingesloten
hoekoppervlakte van 65, maar die is niet te realiseren met gebruikmaking van een pento- en een tetrominoset zonder de tetromino's een andere orientatie te geven"
Ted Lakerveld (Nederland) mailde ons:
Waarschijnlijk zitten onze chocolade-tetromino's nog steeds in Teds verzameling, want we kregen geen betere oplossing. De meest verwonderlijke inzending kregen we van Leon van den Broek (Nederland).
Zijn deze records onjuist of onvolledig,
mail het ons.
Ik vind het een te gek idee om chocolaatjes als puzzelstukjes te gebruiken. Ondanks de verlokking van echte Belgische chocolade, gaan ze mijn verzameling puzzels in. Ze gaven me in ieder geval de inspiratie om toch maar weer met de figuurtjes op mijn scherm te gaan schuiven.
Ik heb voor de kleine hoek een paar kleine verbeteringen ten opzichte van het voorbeeld gevonden, maar die stellen niet veel voor. Ik ben zo als ik al eerder verteld heb niet echt een puzzelaar. Maar zou het helpen als ik die chocolaatjes als nog op eet?

Zijn insluiting had slechts 25 vierkantjes. We begrijpen het nog steeds niet. Of misschien vindt Leon 100 zo'n mooi getal?!
