Symmetry from 1 up to 12 and back

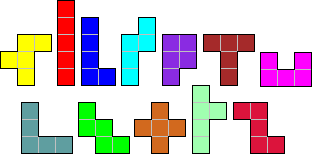
Assign numbers to the 12 pentominoes from 1 up to 12
Make 2 series of 12 shapes, all containing at least one axis of symmetry, with the following conditions:
The shapes may not contain any holes.
Series 1: pentomino 1; pentominoes 1+2; ... ;pentominoes 1+2+...+12.
Series 2: pentomino 12; pentominoes 12+11; ... ;pentominoes 12+...+2+1.
This will be made clearer in the following example.
This example is not a correct solution, as holes are not allowed!



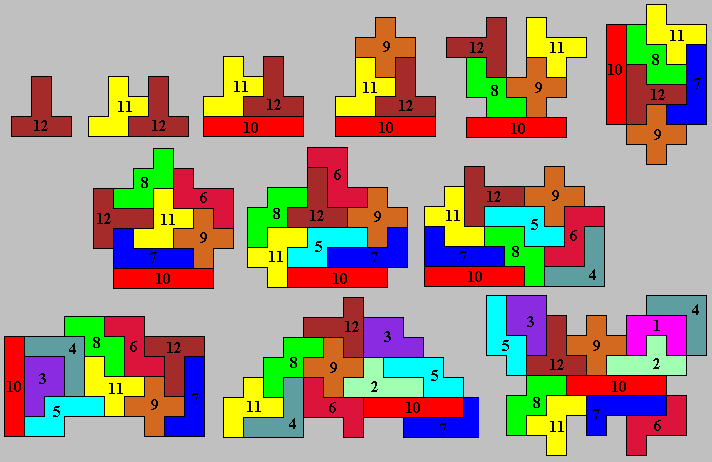
Reinhard Grafl from Austria sent us the last shape, a butterfly.
We started with the U-pentomino and ended with the T-pentomino. The more correct examples you send, the larger the chance that you’ll become the winner.
In case you want an extra challenge, then we invite you to look for solutions for which the total perimeter of all 23 different shapes is either maximal or minimal. (The shape containing 12 pentominoes is counted only once now).
For solving the problem Exel can be used. We have a file containing the pentominoes.