Shaping the largest pento-bridge

Contribution of each pentomino to shaping the rectangular outer border of the bridge.

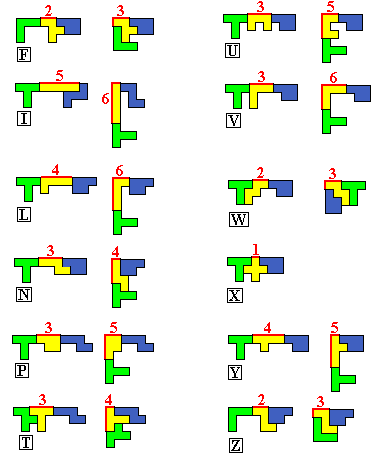
We can see that the best choice leads to 6+6+5+4+3=24 units.
With this our enclosed rectangle should have a maximal area.

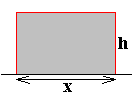
x + 2h = 24 => h = (24 - x) : 2
Area rectangle = f(x) = x.h
f(x)=x(12 -0,5x)
f(x)=-0,5x²+12x
Find out where this function has its maximum.
You can use your TI84 Plus for this (if you don’t have one, you can win one).
Take e.g. as window-settings:
 Xmin=-30; Xmax=30;Xscl=5; Ymin=-100;Ymax=100; Yscl=10

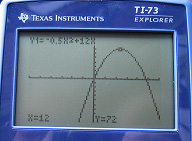
You will find for the value of x at the top 12=>h=6
So we think that a maximal area will be reached if x=12 en h=6.
We make also an exelfile.