37.
Symmetrical chain
Ir
Pieter Torbijn passed away on the 13th of June 2007.

We
decided to dedicate this competition to him. We believe he would have
enjoyed this competition very much considering his compassion for symmetry.
We received the problem from
Stefano Popovski.
When we asked him if he would allow us to dedicate the problem to Pieter
Torbijn, he replied:
"Of course this is
a great loss and for sure you have my permission to dedicate the competition
to Pieter, we all will miss his articles, theoretical comments and valuable
solutions for so many problems! Whatever you think would serve to honor such
a memorable person will be all right."
A
complete set of pentominoes is to be used:
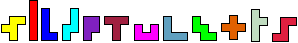
Construct a closed chain using all pentominoes in which every pentomino has
at least two neighbors, where the combination with such a neighbor contains
an axis of symmetry. Thus A and B form a symmetrical shape; so do B and C, C
and D, … K and L and finally L and A as well.
The pentominoes must all be placed in the same flat area, just like the axes
of symmetry.
Stefano sent us an example to clarify the problem.
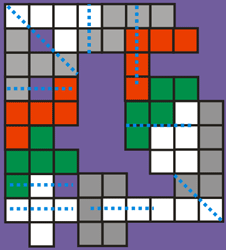
Each blue line indicates an axis of symmetry between two bordering pieces.
Just for the borders between red and green pieces there is no axis of
symmetry present. Try to find as many solutions as possible. We’ll be very
satisfied already when you just find one solution though!
On the next link you can find all combinations of two different pentominoes
that contain an axis of symmetry.
http://pentomino.classy.be/bestanden/symm/allemaal.gif

