39. Pentomino-algebra

Our inspiration is from Peter Hendriks puzzle 206.
Helmut Postl make a similar problem for us.
Aad van de Wetering verified it.
Thanks

The twelve different pentomino pieces have been put together into a 3 x 20 rectangle.

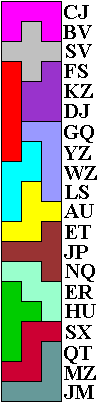
Each of the five squares of every pentomino is going to contain one of the digits 1, 3, 5, 7 or 9. The five digits in a pentomino all should be different. As a result you get a list of 20 three-digit numbers. Each of these numbers can be decomposed into two prime factors.  The two characters in the same row represent these factors. Equal characters represent equal factors, and vice versa. How should the digits be placed in the pentominos? There is only one solution.

To aid in solving the puzzle, Toby makes this applet:
http://www.gottfriedville.net/puzzles/pentprime/index.html