In the third year at KSO Glorieux Ronse we learned about congruency and similarity.
That inspired us to make the following new competition.

Use a set of tetrominoes to make a bridge.

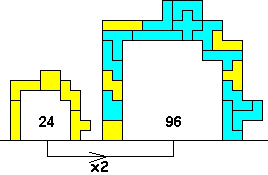
Double all dimensions of the bridge by using a set of tetrominoes combined with a set of pentominoes.
All polyominoes must be in one plane, polyominoes have to touch with at least one full side (just corner connection is illegal).
The enclosed area under the bridge must be one enclosed area.
For the big bridge there’s the extra rule: the tetrominoes may not touch each other, not even with just a corner.
 The main goal is to maximize the enclosed area.
In this example, the tetromino-bridge has an enclosed area of 24, the big bridge is a valid one, it uses the pentominoes + tetrominoes, it is an exact double of the tetromino-bridge, and the tetrominoes are not touching.

Do you have our exel file to draw the bridges? You can download it here.

'FlatPoly2', a programm by Aad van de Wetering, can be of great assistance when trying to find a solution. It can be downloaded at his site .