The idea comes from Aad Thoen living in Amsterdam.
With thanks to Aad van de Wetering for turning the idea into a competition.
For the summer-holidays, we've got two problems, both being a lot of fun according to us.
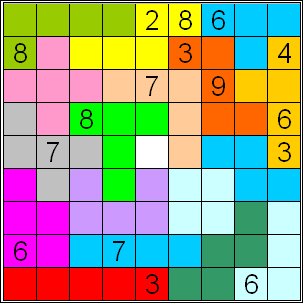
Solve the top sudoku, by taking care the next conditions apply:
◊ numbers 1 upto 9 occur once in each row and column.
◊ The sum of the numbers in the pentominoes must be 25..
◊ The sum of the numbers in de tetrominoes must be 20.
◊ Three numbers a, b and c positioned adjacent to each other as abc (either horizontally, vertically or diagonally) are never allowed to form a sum a + b = c (with a < b), neither a sum a = b + c (with c < b).
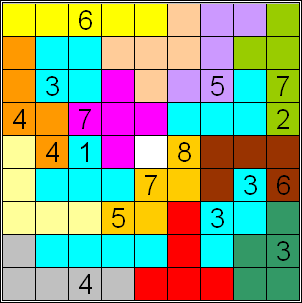
In the second sudoku the 4th condition of the previous one is replaced by:
◊ For three numbers a, b and c positioned adjacent to each other as abc (either horizontally, vertically or diagonally), (b-a) must be different from (c-b). This means that combinations like 123, 963, 159, 333, 468 are not allowed.