In this document you can find all 11 suitable hexominoes.

Draw a positive x-axis and a positive y-axis and build a half bridge from the x-axis down to the y-axis using 6 different 'cubic' hexominoes.
Then draw an enlargement at scale 2 of one of the pentominoes.
Create a second half bridge using this enlarged pentomino and the remaining 5 hexominoes.
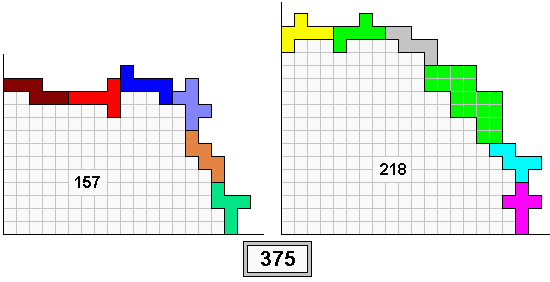
The hexomino's and the enlarged pentomino must lay flat and may not overlap.
Each polyomino must touch at least one other polyomino over a distance 1.
The polyominoes must all fit nicely inside the grid.
The surrounded area must form one part below each of the two half bridges.
Try to maximize the sum of both surrounded areas.
In our example, the sum of the enclosed areas is 375