Records Wedstrijd 47
We kregen een volledige oplossing van de volgende inzenders:
Wil je hun inzending volledig zien, druk dan op hun naam .
We plaatsen telkens één van hun inzendingen.
Bob Henderson - USA

Bob Henderson probeerde de eenzijdigheid van de stukken zoveel mogelijk te respecteren
In het voorgaande voorbeeld is geen enkel stuk omgekeerd gebruikt.

Stefano Popovski - Spanje


Helmut Postl - Oostenrijk


Aad van de Wetering - Nederland

Doel

Berend Jan van der Zwaag - Nederland

Berend Jan stelde een extra voorwaarde aan de doelvorm: deze moet met drie exemplaren van de betreffende pentomino kunnen worden gelegd. Leuk!

We kregen ook deeloplossingen van:
Peter Jeuken
Peter legde zichzelf de beperking op dat het doel een 3x5 rechthoek is.
Dit is het antwoord op vraag 4 van de wedstrijd van Pythagoras
 

Doel

Aad Thoen - Nederland
Van Aad kregen we dit 3x3 geomagisch vierkant met driekleuring

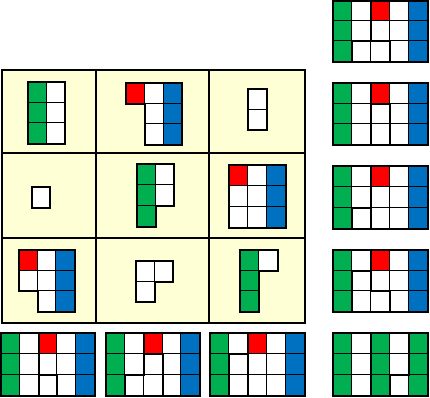
Hij mailde"Er staat maar één pento in, de P. Uit de onvoltooide vierkanten kunt u afleiden dat ik in de foute veronderstelling was dat behalve de centrale pento de overige polyo's onveranderd bleven. Toevallig is zelfs het doel hetzelfde gebleven. Dat is een uitdaging waar ik graag een keer aan ga werken: bepaal een vaste set polyo's van afmetingen 1 t/m 4 en 6 t/m 9 zodat voor elke pento in het centrum een magisch vierkant mogelijk is."
Dit is wel een heel leuk idee maar is het op te lossen?

Michael Dowle - Engeland
"I have attached some magic squares in the attached Word document. Unfortunately I did not get round to completing all the puzzles."

Doel

Frasquelo T'Sjoen

Doel

Arno Stockman

Bij vaststelling van fouten of onvolledigheid, mail naar:
o.d.m@fulladsl.be