48. Symmetric-competition of Popovski Thanks to Stefano Popovski for the idea of this challenge.

You have the set of 12 pentominoes and you work strictly on a plane.

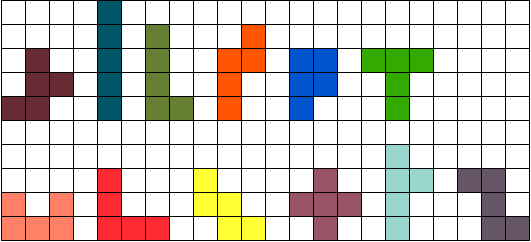
Divide this set to make 4 groups of 3 pentominoes in each. You are free to choose which pentominoes will go in every group.
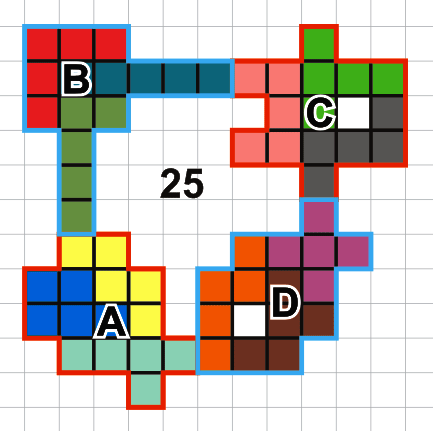
Arrange the 3 pentominoes in each group to make a symmetrical shape. It's completely up to you to decide the form of the shapes. From the resulting 4 symmetrical "15-minoes" (A,B,C,D in the example) form the maximal possible farm.
The example shows a farm of 25 squares. Try to find the maximal.
Each group has to touch the neighbour groups along the length of at least 1 minimal square. Inner holes in the groups (like C and D in the example) doesn't count as part of the farm.

May be you find some help on http://pentomino.classy.be/symmphilo.html (In Dutch)