49.
Two holes problem
Searching our archive for inspiration for a new problem, we noticed the
following problem from the Journal of Recreational Mathematics - 1987,
by Stan Vejmola from Prague.
Use a set of pentominoes to create a fence enclosing two areas, such
that the sum of the enclosed areas is maximal.
The
non-overlapping pentominoes have to lie on the grid and in the same
plane, and touch each other with at least one side.
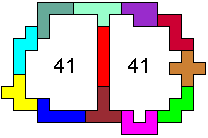
Sergio Stanzani made the following solutions:
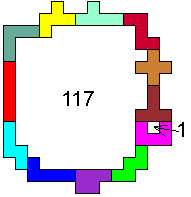
Our friend Pieter Torbijn († 2007) made the following solutions:
|
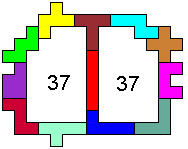
With two congruent areas |
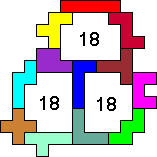
With three congruent areas |
Aad van de Wetering improved one record. Congratulations
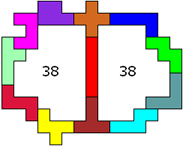
For our contest 49 we state the same problem with the same conditions
except the set of pentominoes, which is the set of one-sided pentominoes: