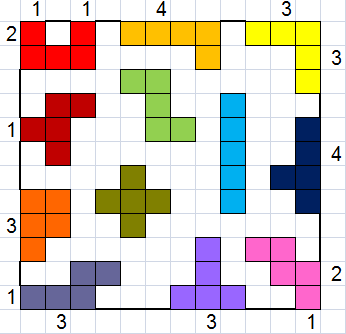50. Anniversary Contest
To our call for a nice match statement we received many responses.
Many thanks for all the great problems we have got.
Therefore, we thought we let the solver choose.
We hope that we have not forgotten anyone. Else send an email.
This is probably our last competition.
We
start with the problem
of Kate
Jones
because we
got
the following
mail "Attached is a "50" puzzle I designed some time ago, one copy of
which we will be happy to give as a prize for your winner. It is a $45
value and contains all the polyominoes 1 through 5. It has many
solutions and is based on our Poly-5 puzzle,
www.gamepuzzles.com/polycub2.htm#P5"

We thank Kate and
Kadon Enterprises for the prize.
Problem of
Kate Jones.

Fit all the polyominoes from 1 through 5 into the grid within the
number 50, so that no two of the tetrominoes, trominoes, the domino and
monomino touch each other, not even at the corners. It's not difficult
but very pretty!
Kate:"I would like to know whether it was solved by a computer or by
a human!"
To help you with solving we made
an
excel file
and also
a geogebra applet.
If you have questions about them, just ask
o.d.m@fulladsl.be
Flat
Poly
calculated
that there are
many
different
solutions.
You
can
download
FlatPoly
at
http://home.wxs.nl/~avdw3b/aad.html

The idea of our 34th
competition is also by Kate Jones.
Problem of Bob Harris
(A) Choose a pentomino and make 13 copies of it, colored
yellow, and choose a tetromino, and make 4 copies of it,
colored black.
(B) Place the pieces so that a 7x7 square is covered to a "depth" of 1.
The yellow pieces are "positives" and count as +1; the black pieces are
"negatives" and count as -1. Pieces may be placed on top of each other
and wherever this occurs a black cell will cancel a yellow one. For example, a cell
covered by a single yellow piece has a depth of 1, as will have a cell
covered by two yellows and one black piece.
Pieces needn't stay within the 7x7 square, but any cell outside the
square must have a depth of zero (which usually means that it is covered
by a single yellow and a single black piece).
Bob's motivation for this problem: "I've been investigating polycube puzzles made
from several copies of two (or three) pieces. One such puzzle has been
on my website for years:
http://www.bumblebeagle.org/polycubes/7andF.solution.gif
Now, if I want to have a heptacube and a pentacube fill a 4x4x4, how
many copies of each would I need? This is solved by 7a + 5b = 64,
looking for positive integer solutions. Integer solutions are a=7-5k
b=3+7k (for some integer k), and restricting this to positive integers
the only solutions are a,b=7,3 or a,b=2,10.
Looking at the same sort of thing in 2D, suppose I want to pack a 7x7
with pentominoes and tetrominoes. Then I have 5a+4b = 49 with integer
solutions (a,b)=(9-4k,1+5k). Solutions in positive integers are (9,1),
(5,6), (1,11). But there are also solutions with negative integers. In
this
example is (a,b) = (13,-4), or 13 pentominoes and negative
4 tetrominoes.
We choose the L-pentomino and the L-tetromino.
Use the mouse pointer to see the example

Can
you do it with
the
other
pentominoes?"
Problem of
Martin Watson.
The idea of our
21th
competition is also of Martin Watson.
Place the 12 pentominoes in a 12x12 square so
that no two pentominoes
touch each other, not even corner to corner.
Count how many edges of the square (12x4=48 in total) are touched by the
pentominoes. What are the maximum and minimum values? In the example
below this value is 32 (1+1+4+3 = 9 units at the top edge, and so on.)
Notice that a pentomino cell which covers a corner of the square counts
for 2 edges.
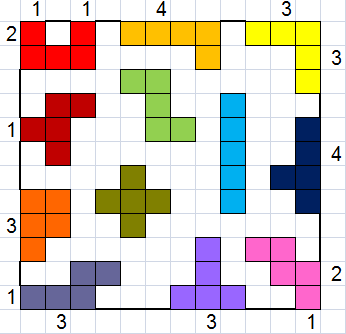
Problem of Peter Jeuken
Peter created this pentomino puzzle especially for us.
12 sets of 12 pentominoes and 12 sets of 5 tetrominoes together form a
32x32 square where the four corners (4x4 squares) are missing.
If you prefer to see it larger, then click on the picture.

Cut the figure into 12 pieces so that each piece contains exactly 12
different pentominoes and 5 different tetrominoes.
Only cuts along the grid lines are allowed. Pentominoes and tetrominoes
must not be cut in two.
If you find more than one solution, then submit the solution with the
smallest total perimeter of the 12 pieces.
Problem of Aad Thoen : Pentomino-
islands
Place all pentominoes as islands in a sea such that the area of
this sea should be as small as possible. The pentominoes must not touch
each other, not even at the corners.
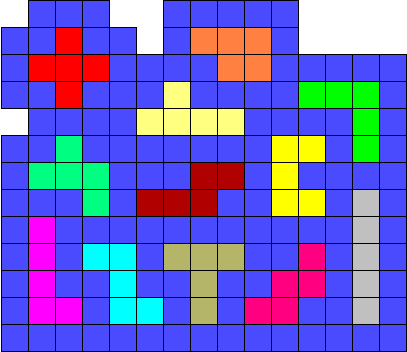
In our example the sea area is 122 units.
A variant of this problem is us
potpourriproblem 11 (Dutch) where the
sea has to be a rectangle.
Another problem is that we allow the pentominoes to be peninsulas.
Problem of Aad van de Wetering
We would like to thank Aad van de Wetering very much for doing a
great job in establishing our pentomino site.
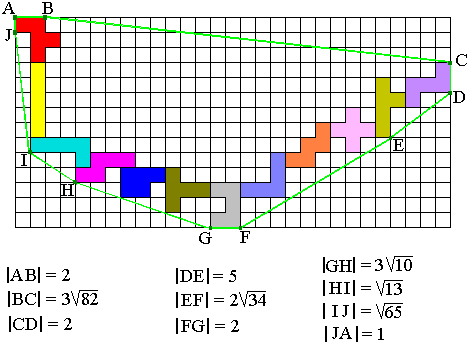
1 + 1 = 3
This problem was created by our friend Pieter Torbijn to whom we
dedicate the whole competition.
Enclose a set of pentominoes with two other sets. Make the area of the
circumscribed rectangle as small as possible.
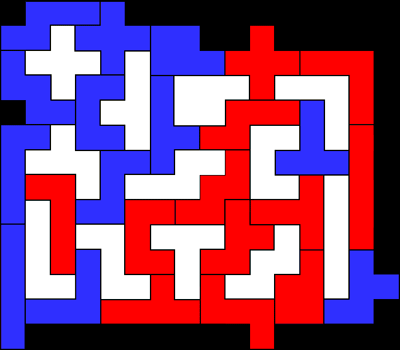
In our example the rectangle is 16 x 14.
You can find another solution of Michael Keller on
http://www.solitairelaboratory.com/pentmino.html.
This solution is a rectangle of 18 x 13. One can do much better.
Pento-Product-Xudoku
On request, because we know we have many visitors who love sudoku,
Aad van de Wetering made for us this great hint free xudoku.
Put the numbers from 1 to 8 in each row, in each column and in
the two diagonals.
The products of the numbers in each pentomino are as follows:
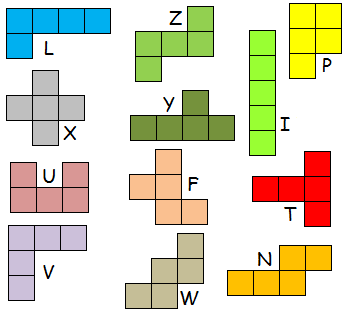
L:420, X:96, U:1080, V:11760, Z:576, Y:336, F:1440, W:84, P:720, I:1120,
T:384 , N:1680
Would you like a hint? Mail to
o.d.m@fulladsl.be
'50.
Fifty-Fifty'
Competition by Edo Timmermans
We asked Edo to create a competition for our 50th Jubilee because
we consider him to be one of our most creative problem creators. (see
the Pentomino postcard
competition and the
Isle of count Penteviticole)
His competition consists of 2 parts.
Take a red 10x10-square with a diagonal green square inside having 50%
of the surface of the 10x10-square. The pentominoes are to be placed
within the big square in such a way that they are all partially red and
partially green.
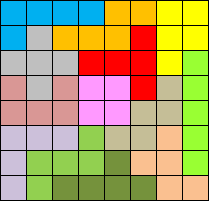
In the first 50% of the competition, you are invited to search for
solutions where 10 pentiminoes are 50% red and 50% green. Also, all
pentominoes together must be 50% red and 50% green.
The examples show that this is not very difficult when the remaining 2
pentominoes are allowed to be 10% red or 10 % green. That is why these 2
pentominoes must minimally be 20% red as well as minimally 20% green,
yet the closer to 50% the better, of course.
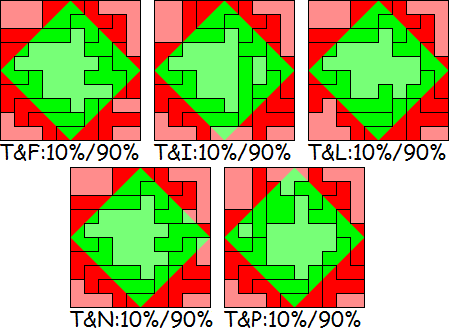
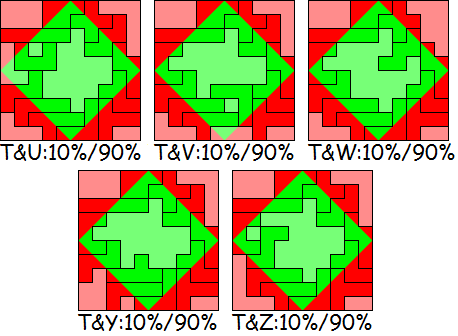
In the second 50% of the competition you are invited to look for a
symmetrical solution. The demand that 10 pentominoes must be half red
and half green is dropped, but each pentomino must still be partially
red and partially green.
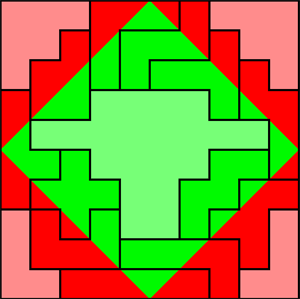
The
example is not a valid solution, only because the W-pentomino is
entirely green.
Computer programmers are invited to look for symmetrical solutions where
at least 50% of the pentominoes are 50% red and 50% green.
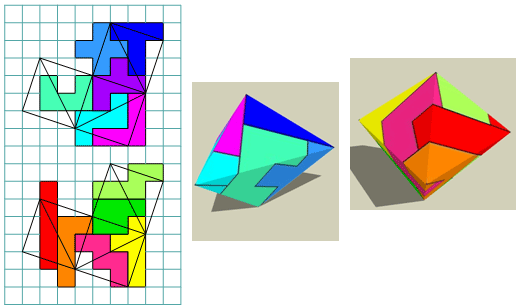
Pentorigami-Problem of Bob Henderson
Cut 12 pentominos from stiff
paper of different colors.
For your convenience, we put 6 copies of each pentomino on a sheet.
So you get different
sets of pentominoes
F
I
L
N
P
T
U
V
W
X
Y
Z
Cut 1 of the 4 grid lines that meet at the center of P.
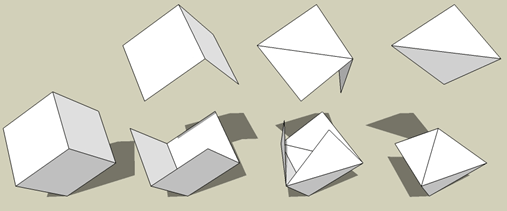
There are eight pentominoes which can be folded into an open cube (a
cube without top face). They are F,L,N,T,W,X,Y and Z.
Take 6 of these 8 open cubes and join them at the edges of their
openings. They will look like 6 cubes attached to the faces of a seventh
(hidden) cube.
|
 |
 |
Now take the I,P,U and V pentominoes together with the two remaining
pentominoes. Fold and join these 6 pieces to build the same shape as you
did before with the other 6 pentominoes.
To build the second shape, all six pentominoes may be folded arbitrarily
along the grid lines, they need not form open cubes.
3D-Problem of Michael Dowle
Cover a cube of edge length √10 with a pentomino set.
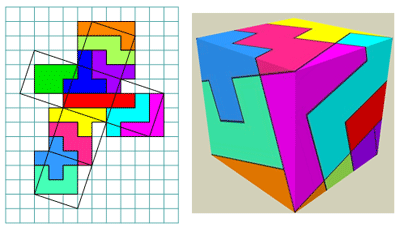
During several
years
students of KSO
Glorieux Ronse (Belgium) cover
a
cube
for
their
work
of
Pythagoras.
http://www.pentomino.classy.be/versnijdenopkubus.html