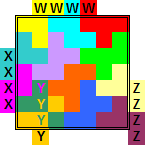
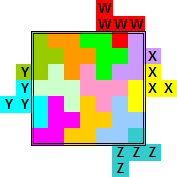
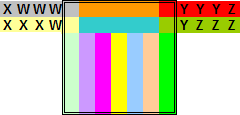
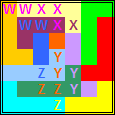
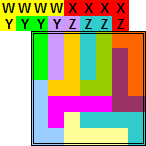
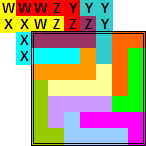
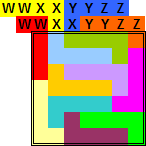
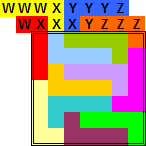
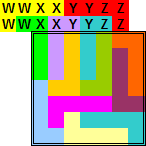
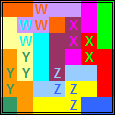
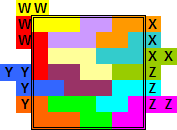
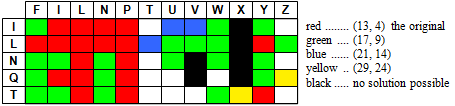
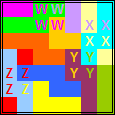Oplossingen van de opgave van Bob Harris
We beginnen met de inzending van Helmut Postl (hij was de enige die voor de beide opgaven iets inzond.)
Wat is dit een knappe inzending!!!
Original Task: Take 13 copies of a pentomino and 4 copies of a tetromino.
Choosing one of the 12 pentominoes and one of the 5 tetrominoes yields 60 subproblems.
I tried to find solutions for as many subproblems as possible. If I did not find a solution for (13,4), I tried the weaker condition of raising the numbers of pentominoes and tetrominoes.
The following table gives a summary of solutions which I have found so far:
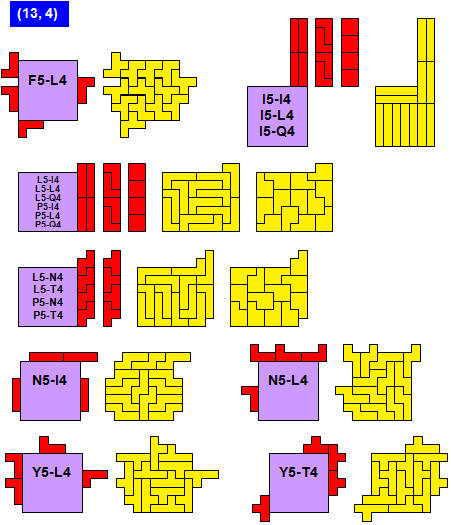
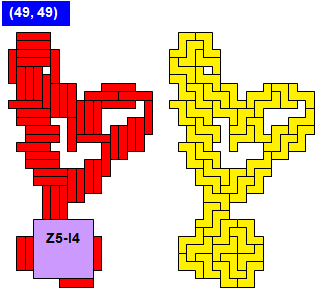
Proof that X5 cannot be combined with I4, L4, N4 or Q4.
Make a checkerboard colouring. The 7×7-square has 25 white cells and 24 black cells (WLOG). The tetrominoes contribute as many white as black cells to the whole pattern. So the pattern has one more white cell than black ones, i.e. W – B = 1.
On the other hand, the X5 has 1 white and 4 black cells, or vice versa. This means that the difference of white minus black cells is divisible by 3. This carries over to the whole pattern since it can be tiled by X5’s only. Therefore, |W – B| is a multiple of 3. But this contradicts W – B = 1. QED
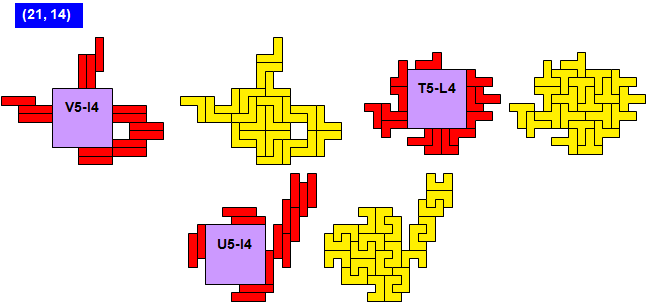
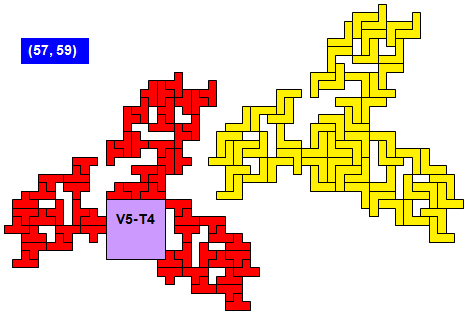
Proof that V5 cannot be combined with N4 or Q4.
Make a stripe colouring, that is alternating black and white infinite stripes of width 1. Then the same argument as above holds. On the one hand, W – B = 7, and on the other hand, |W – B| is a multiple of 3. Contradiction. QED
Ongelooflijk: na 14 dagen kregen we een nieuwe mail van Helmut met nog meer (schitterende) oplossingen.
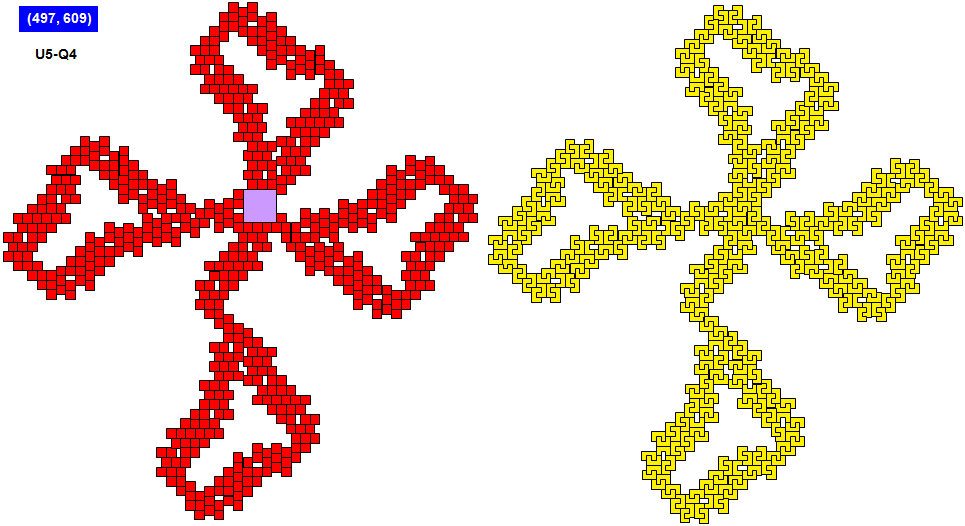
"I can’t believe it, but I really managed it to solve all 60 subproblems of Bob Harris’ task. By far the most difficult case was the U5-Q4. Long time I thought that there is no solution. And I tried to prove it. But I could not perform the proof. In the end, this was very helpful in getting some insight which constellations may be possible. And I got more and more convinced that the problem has a solution. And after looking for a long time, I finally have found one. Gosh! I am pretty sure that there is a smaller pattern, but at least, there is a pattern at all. Have fun with it!"
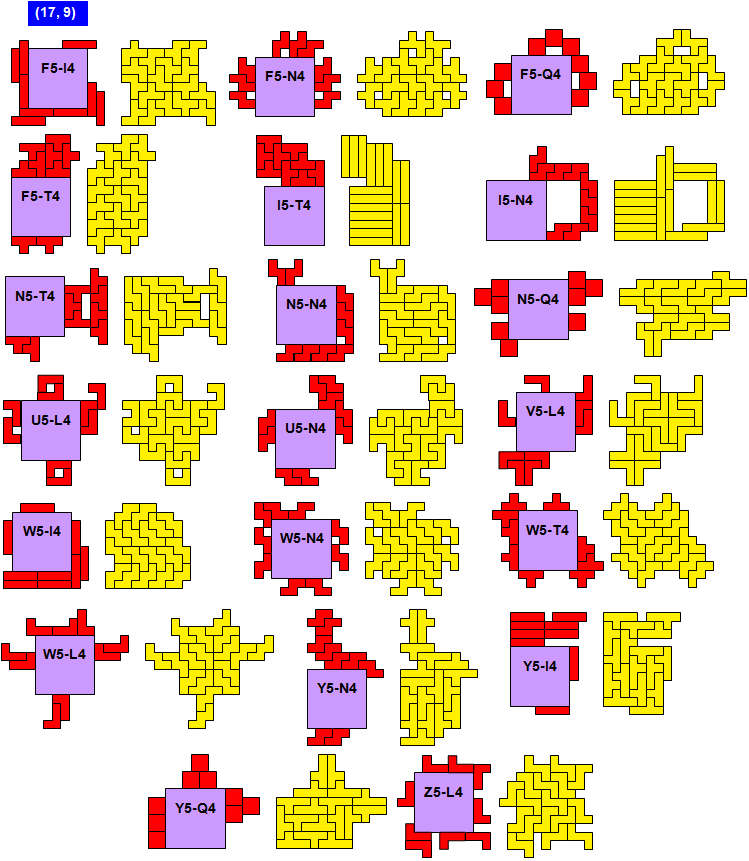
Here are some new results and the updated table.
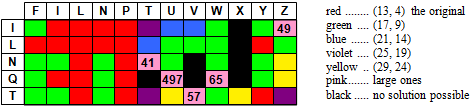
The pink entries mean some large solutions. This shall demonstrate that a solution exists at all. The number in the pink cell indicates the number of pentominoes used. I don’t know if and how far these numbers can be reduced.
.png)
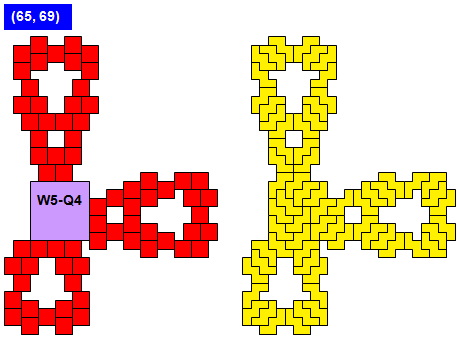
Proof that T5 cannot be combined with Q4.
Make a stripe colouring in three colours, that is alternating black, white and red infinite stripes of width 1.
The 7×7-square covers (WLOG) 21 black, 14 white and 14 red cells. The appended Q4-tetrominoes cover 2 cells of two colours and none of the third colour. That means that the even/odd-parity of the three colours remain invariant – the pattern always covers an odd number of black cells and an even number of white and red cells, that is (odd/even/even).
On the other hand, a T5-pentomino covers always 3 cells of one colour and 1 cell of the other two colours, no matter how it is placed. That means that each appended T5 changes the parity of all three colours simultaneously. Starting with an empty pattern which has parity (even/even/even), we can achieve only (even/even/even) and (odd/odd/odd). Therefore it is impossible to achieve (odd/even/even). QED
Ongelooflijk: na 6 weken kregen we nog een aanvulling van Helmut.
"I have found some new results to the problem of Bob Harris. Since some pentominoes may be superimposed, I found constellations for the T, U, V and W pentominoes which lie completely within the 7x7-square. The X and the Z are still missing, I did not find anything so far."
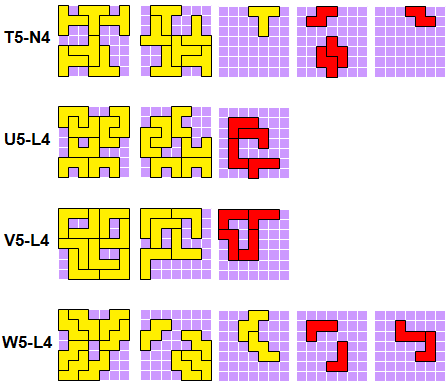
Task variant: Take all 12 pentominoes together with an extra one, and take 4 out of the 5 tetrominoes.
Choosing one of the 12 pentominoes as the extra one and one of the 5 tetrominoes to omit yields 60 subproblems.
My solution: I found two shapes which can be filled with every choice of 4 tetrominoes. (One single shape is not possible because of different checkerboard parities.) These shapes are glued to the 7×7-square to build the instances of the whole pattern which have to be filled with the 13 pentominoes.
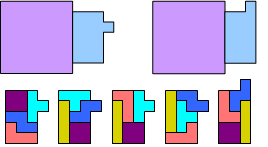
Both patterns can be filled with the 12 pentominoes and every choice of the extra pentomino. These patters are built from the same subpattern together with the P pentomino which comes in two orientations. The subpattern can be filled in every desired way.
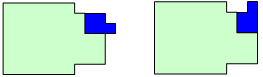
Remark: I looked for solutions where the two identical pentominoes do not touch.
Van Aad van de Wetering kregen we er eentje: "Heeft Bob voor elke pentomino een oplossing gevonden? Ik was een tijdje bezig met de Y, maar vond niets. De P is daarentegen erg gemakkelijk, evenals de I. Maar de andere…"
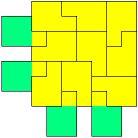
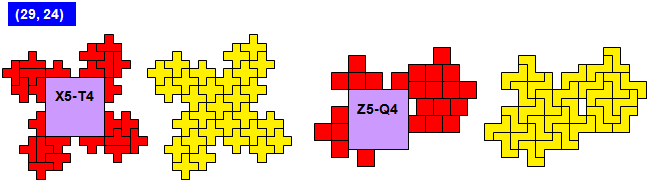
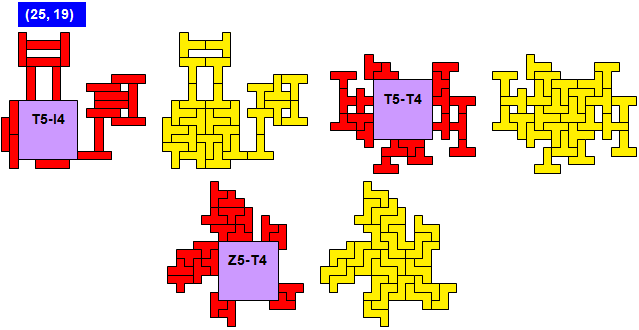
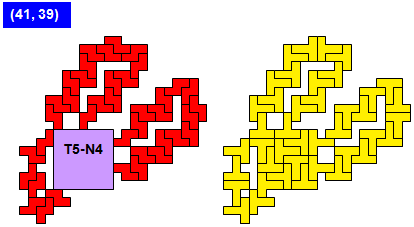
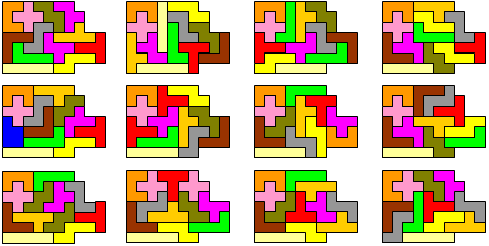
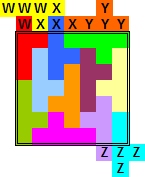
Van Berend Jan van der Zwaag kregen we de volgende oplossingen van (13,4)
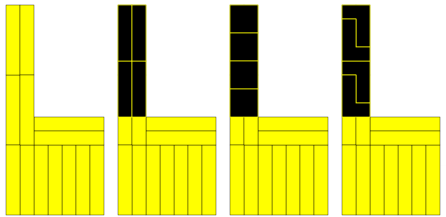
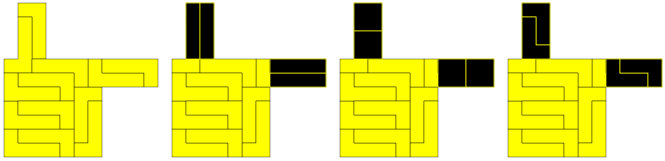

Oplossingen van Dario Uri:"I find the Bob Harris's problem very interesting. I attach six solutions. The black lines above the sketches connect the centers of the tetraminoes."
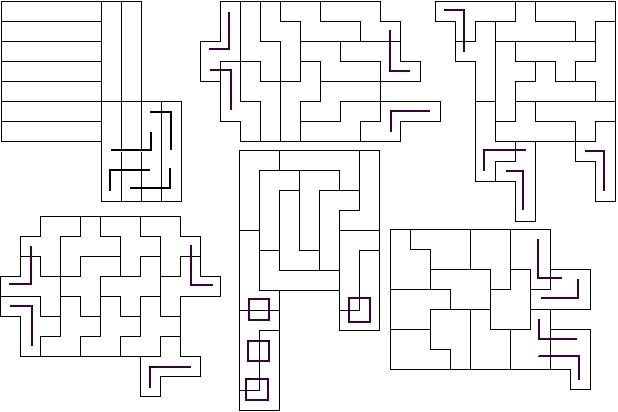
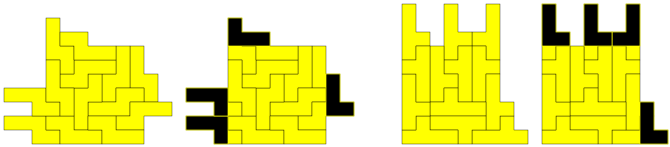
Van Bob Henderson kregen we de volgende oplossingen van (13,4)
|
|
|
|
|
|
|
|
|
|
|
None Found |
None Found | None Found |
|
|
|
|
|
|
|
|
|
|
|
None Found |
None Found |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
None Found | None Found | None Found |
|
|
 |
 |
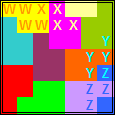 |
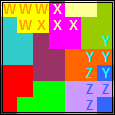 |
|
|
|
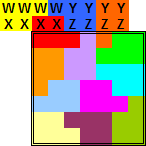 |
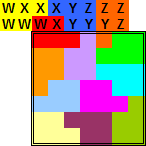 |
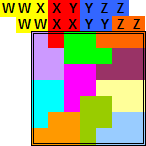 |
 |
 |
|
|
None Found | None Found | None Found | None Found | None Found |
|
|
 |
 |
 |
 |
None Found |
|
|
None Found |
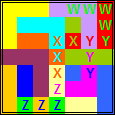 |
None Found | None Found | None Found |
|
|
None Found | None Found | None Found | None Found | None Found |
|
|
None Found | None Found | None Found | None Found | None Found |
|
|
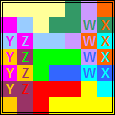 |
 |
 |
 |
 |
|
|
None Found | 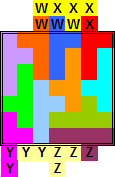 |
None Found |
 |
None Found |
|
|
None Found | None Found | None Found | None Found | None Found |
Bij vaststelling van fouten of onvolledigheid, mail
naar:
o.d.m@fulladsl.be