Sorry I didn't do your competition before.
It's easy to prove the best solution.
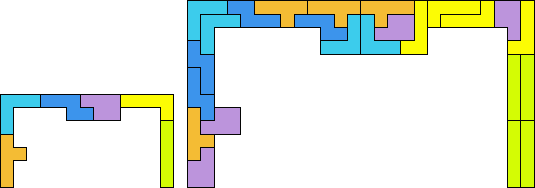
The maximum contribution to perimeter for each piece is: (if 2 figures are given, the first is for placing the piece in a top corner, and only two of these can be chosen)
I 5
L 5,4
V 5,3
Y 4
P 4,3
N 3
U 3
T 3
W 2
Z 2
F 2
X 1
So maximum 'perimeter squares' is 5+5+5+4+3+3 or 5+4+5+4+4+3 = 25. Since two corner squares contribute to width as well as height, we have a real maximum perimeter of 27.
This gives a maximum area when width is closest to double the height, as can be seen by the maximum area for each of:
Height Width Area
5 17 85
6 15 90
7 13 91
8 11 88
9 9 81
So the best we can hope for is area 91 (less area of 6 pentominos, equals 61)
My program found 792 ways of tiling the 7*13. Choosing a likely solution: