Bob Henderson USA
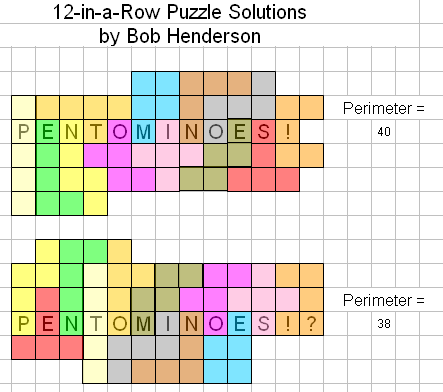
"I tried to match Helmut's solutions to Kate Jones' puzzle by hand and quickly found an 80 perimeter. I could only get down to 42 by hand, but with some help from my computer I found several solutions with a perimeter of 38! Some program output is attached below. I assumed that there should be no interior holes, but that one pentomino may cover a 13th (blank) space in the same row as "PENTOMINOES!". Let me know if these assumptions satisfy the intended puzzle requirements. Thanks again!"

We keuren dit af. We vinden dat dit niet aan onze eis voldoet :" ...zodanig dat er binnen de figuur een lijn is die bestaat uit juist 12 vierkantjes die van alle pentomino's juist één vierkantje bevat."
We hadden echter de tijd niet gevonden om Bob hiervan te verwittigen en kregen een volgende mail:
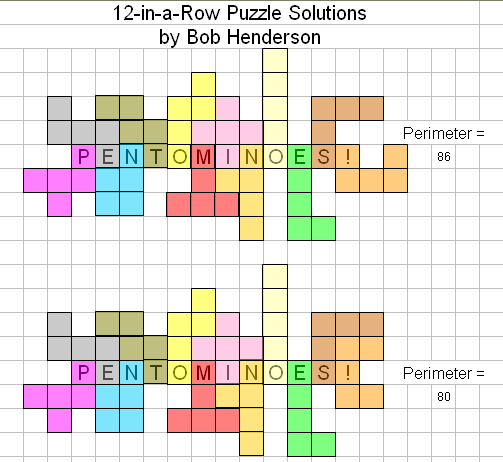
"I have found many solutions with a maximum perimeter of 86 units for Kate Jones' "12 in a row" puzzle. They all have an empty space at each end of a row of 12 spaces occupied by 12 different pentominoes, which seems to meet the contest puzzle requirement of 'a line of exactly 12 squares' . If it is required that no spaces beyond the ends of the row may be occupied, the U pentomino at the end may be turned to put its middle square at the end of the row. This brings 3 more of its faces into contact with the other pentominoes, reducing the total perimeter to 80 units (the same answer that Helmut found). The attached Excel file shows an example of each case.
The solutions with a perimeter of 38 units that I sent to you earlier also contain 12 different pentominoes in a row of 12 consecutive squares, but the U pentomino also occupies a 13th square at the end of the row. If this does not meet the contest puzzle requirement above, please see the attached Excel file for a solution with a perimeter of 40 units (again, the same as Helmut found). Many thanks to you and Kate Jones for this nice puzzle!"