Brugprobleem 5:
Bouw met een set pentomino’s een brug met als buiten- en een binnenomtrek een rechthoek.
De oppervlakte van de ingesloten rechthoek moet zo groot mogelijk zijn.
Met heel veel dank aan
Aad van de Wetering
voor het krijgen van zijn programma”FlatPoly”
waarmee we deze oplossingen gemakkelijk kunnen vinden.
 Extra voorwaarde:de buitenomtrek van de brug moet een vierkant zijn
en moet een symmetrie as zijn voor binnen- en buitenomtrek van de brug.
Extra voorwaarde:de buitenomtrek van de brug moet een vierkant zijn
en moet een symmetrie as zijn voor binnen- en buitenomtrek van de brug.
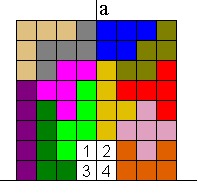 We kregen 2 varianten op dit probleem:
van Aad van de Wetering, Driebruggen, Nederland.
Bouw met een set pentomino’s een brug met als buitenomtrek
een vierkant en als binnenomtrek een rechthoek.
De oppervlakte van de ingesloten rechthoek moet zo groot mogelijk zijn.
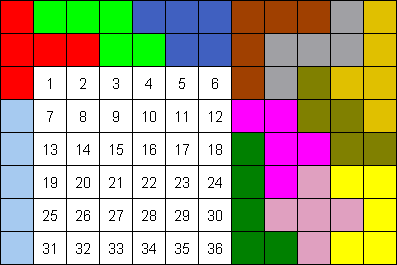
Aad stuurde ons een oplossing waarbij de rechthoek een oppervlakte heeft van 40 eenheden.
We kregen 2 varianten op dit probleem:
van Aad van de Wetering, Driebruggen, Nederland.
Bouw met een set pentomino’s een brug met als buitenomtrek
een vierkant en als binnenomtrek een rechthoek.
De oppervlakte van de ingesloten rechthoek moet zo groot mogelijk zijn.
Aad stuurde ons een oplossing waarbij de rechthoek een oppervlakte heeft van 40 eenheden.
 Van Helmut Postl, Wenen, Oostenrijk.
Bouw met een set pentomino’s een brug met als buitenomtrek
een rechthoek en als binnenomtrek een vierkant.
De oppervlakte van het ingesloten vierkant moet zo groot mogelijk zijn.
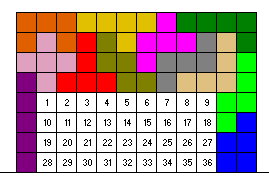
Helmut stuurde ons een oplossing waarbij het vierkant een oppervlakte heeft van 36 eenheden.
Van Helmut Postl, Wenen, Oostenrijk.
Bouw met een set pentomino’s een brug met als buitenomtrek
een rechthoek en als binnenomtrek een vierkant.
De oppervlakte van het ingesloten vierkant moet zo groot mogelijk zijn.
Helmut stuurde ons een oplossing waarbij het vierkant een oppervlakte heeft van 36 eenheden.
 Extra voorwaarde:de buitenomtrek van de brug moet een vierkant zijn
en moet een symmetrie as zijn voor binnen- en buitenomtrek van de brug.
Extra voorwaarde:de buitenomtrek van de brug moet een vierkant zijn
en moet een symmetrie as zijn voor binnen- en buitenomtrek van de brug.
 We kregen 2 varianten op dit probleem:
van Aad van de Wetering, Driebruggen, Nederland.
Bouw met een set pentomino’s een brug met als buitenomtrek
een vierkant en als binnenomtrek een rechthoek.
De oppervlakte van de ingesloten rechthoek moet zo groot mogelijk zijn.
Aad stuurde ons een oplossing waarbij de rechthoek een oppervlakte heeft van 40 eenheden.
We kregen 2 varianten op dit probleem:
van Aad van de Wetering, Driebruggen, Nederland.
Bouw met een set pentomino’s een brug met als buitenomtrek
een vierkant en als binnenomtrek een rechthoek.
De oppervlakte van de ingesloten rechthoek moet zo groot mogelijk zijn.
Aad stuurde ons een oplossing waarbij de rechthoek een oppervlakte heeft van 40 eenheden.
 Van Helmut Postl, Wenen, Oostenrijk.
Bouw met een set pentomino’s een brug met als buitenomtrek
een rechthoek en als binnenomtrek een vierkant.
De oppervlakte van het ingesloten vierkant moet zo groot mogelijk zijn.
Helmut stuurde ons een oplossing waarbij het vierkant een oppervlakte heeft van 36 eenheden.
Van Helmut Postl, Wenen, Oostenrijk.
Bouw met een set pentomino’s een brug met als buitenomtrek
een rechthoek en als binnenomtrek een vierkant.
De oppervlakte van het ingesloten vierkant moet zo groot mogelijk zijn.
Helmut stuurde ons een oplossing waarbij het vierkant een oppervlakte heeft van 36 eenheden.
