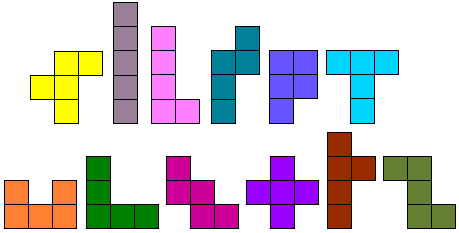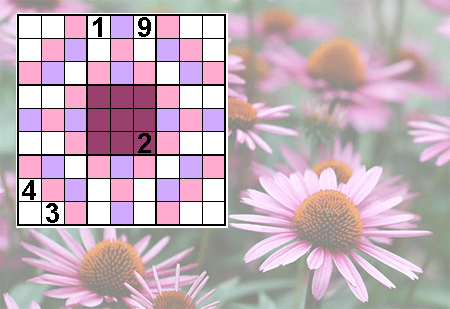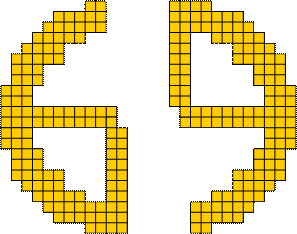Cijfers met pentomino's
Kan je het beter?
Mail een 'cijfer' naar
OdetteDM@outlook.com
Misschien belonen we wel met een chocolade 'cijfer'
George Sicherman dacht dat hij beter
kon.
Hij mailde:"5 of your digits lack unique solutions.
Permit me to remedy this."
Behalve "9" vinden we deze cijfers niet zo mooi maar de oplossing is wel
enig.
Van Helmut Postl kregen we alle cijfers met een unieke oplossing op 26/10/2016 maar op 18/11/2019 herinnerde hij ons eraan en dus gingen we op zoek en vonden het terug.

Sylvie Razafindrakoto.
Ze maakte haar gelukscijfer "5"
Grote
getallen in sudoku's en pentomino's
We vroegen aan Helmut of hij iets leuk kon
bedenken met "70" (voor de verjaardag van Aad van de Wetering 16
november 2014) en we kregen
een schitterende sudoku verbonden met heel wat pentominoproblemen.
De volgende sudoku heeft de bijkomende eigenschap dat de som van de getallen
in de rode vakjes 70 is.
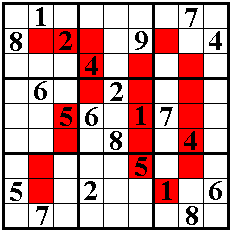
Goede oplossers verwerven eeuwige roem.
Mail naar:
OdetteDM@outlook.com
| Naam |
Land |
| Helmut Postl |
Oostenrijk |
| Aad Thoen |
Nederland |
| Aad van de Wetering |
Nederland |
| Odette De Meulemeester |
België |
| Sander Waalboer |
Nederland |
| George Sicherman |
USA |
| Nico Looije |
Nederland |
| Bob Henderson |
USA |
| Matthijs Coster |
Nederland |
| Peter Jeuken |
Nederland |
| Martin Friedeman |
Nederland |
George Sicherman:"I solved them by computer. Doing it by hand would take
too much trial and error, and I already have enough trial and error in my
life!"
Het hoeft geen gissen en missen te zijn want je kan redeneren!
Bob Henderson: "I found the following results by modifying my Sudoku
solver to run until the marked cells had the correct sums. I did not search
for any more solutions: I have no doubt that Helmut designed them to have
only one!"
Er is inderdaad maar één oplossing maar je kan elk getal vinden door te
redeneren.
Verder zijn er 60 witte vakjes die kunnen bedekt worden
met 12 pentomino's. Jammer genoeg is dit niet mogelijk met een set
pentomino's.
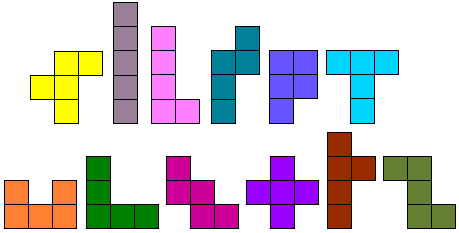
Er zijn echter wel andere interessante mogelijkheden:
1)Kies 4 pentomino's en gebruik die elk drie keer. Er bestaat maar één
keuzemogelijkheid en er zijn
twee oplossingen
2) 9 is het grootste aantal verschillende pentomino's
waarmee je de witte vakjes kan vullen.
Eén van die combinaties heeft maar juist één oplossing. Druk
hier voor die oplossing.
3)3 is het kleinste aantal pentomino's die we kunnen
gebruiken. Je mag een willekeurig aantal exemplaren van elk gebruiken. Er is
juist
één oplossing.
4) Het grootste aantal exemplaren van eenzelfde pentomino is 8. De
resterende 4 stuks hoeven niet verschillend te zijn. Er zijn
twee oplossingen die op elkaar lijken.
Een ander idee is de twee horizontale randen samen te plakken zodat je een
cilinder bekomt. Er zijn echter nog steeds geen oplossingen om de witte
vakjes op te vullen met een pentominoset.
Ook is er geen oplossing als we een cilinder maken door de verticale randen
samen te plakken.
Als we echter zowel de horizontale als de verticale randen samen plakken,
dus een torus maken zijn er 105 oplossingen.
|
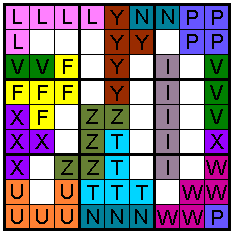
4 pentomino's liggen over de randen
(kleinste aantal)
|
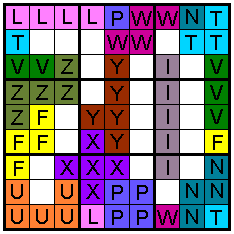
8 pentomino's liggen over de randen. er zijn 9 stukken die over de
randen gaan
(grootste aantal) |
Helmut stuurde
een tekstbestand met alle oplossingen.
Hierin kan je de oplossingen vinden door respectievelijk te zoeken naar "4A"
en "9A" om het minste en het meeste aantal overlappende stukken van
pentomino's te vinden
Helmut maakte er een gelijkaardige voor 64. (10 oktober
2014)
De sudoku heeft de bijkomende eigenschap dat de som van de getallen
in de rode vakjes 64 is.
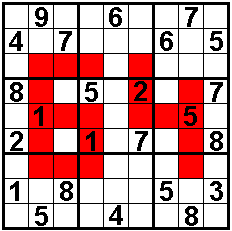
Goede oplossers verwerven eeuwige roem.
Mail naar:
OdetteDM@outlook.com
| Naam |
Land |
| Helmut Postl |
Oostenrijk |
| Aad Thoen |
Nederland |
| Aad van de Wetering |
Nederland |
| Odette De Meulemeester |
België |
| Sander Waalboer |
Nederland |
| George Sicherman |
USA |
| Nico Looije |
Nederland |
| Martin Friedeman |
Nederland |
| Bob Henderson |
USA |
| Peter Jeuken |
Nederland |
Aad van de Wetering: "Voor de
64 (ook een idee) had ik geen software, met Xudoku alle oplossingen gemaakt
en Excel laten uitrekenen welke som 64 had voor de gevraagde vakjes. Dat was
er één, alle andere hadden een grotere som."
Sander Waalboer zal daar wel software voor hebben want op 10 min stuurde
hij zowel een oplossing voor "64" als voor "70" terug
Nico Looije: "Dit is een leuk idee. Ik moest een minimale programmatische
aanpassing doen om ze op te lossen"
Verder zijn er 60 witte vakjes (het witte vakje in de rode 6 laten we
buiten beschouwing) die kunnen bedekt worden
met 12 pentomino's. Jammer genoeg is dit niet mogelijk met een set
pentomino's.
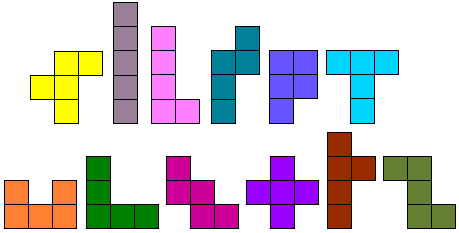
Er zijn echter wel andere interessante mogelijkheden:
1)Kies 6 pentomino's en gebruik die elk twee keer. Er zijn veel
mogelijkheden.
Probeer een set te vinden enerzijds zonder de L-pentomino en anderzijds
zonder de P-pentomino.
Zonder L-pentomino zijn er 2 combinaties.
INPTWY: 3 oplossingen
INPUVY: 1 oplossing
Zonder P-pentomino zijn er 2 combinaties.
ILNTVY: 2 oplossingen
ILNTVW: 1 oplossing
2) Kies 4 pentomino's die je elk driemaal gebruikt.
Er is maar één combinatie die
drie verschillende oplossingen heeft.
3)Het grootste aantal verschillende pentomino's die men kan gebruiken is 10.
Er zijn veel verschillende mogelijkheden.
Drie combinaties hebben juist één oplossing:
één zonder de L-pentomino, hierbij wordt
één pentomino driemaal gebruikt
één zonder de N-pentomino, van de
P-pentomino en I-pentomino gebruiken we twee exemplaren.
één met de X-pentomino, van de P-pentomino
en I-pentomino gebruiken we twee exemplaren.
4) Het kleinste aantal verschillende pentomino's dat men kan gebruiken is 4.
Hier zijn heel wat mogelijkheden.
Eén combinatie is echter uniek; deze
combinatie bevat de Z-pentomino
5)Het maximum aantal kopieën van éénzelfde pentomino die men kan gebruiken
is 8. De overige 4 pentomino's moeten niet noodzakelijk verschillend zijn.
Er zijn vier verschillende combinaties maar allemaal met 8 kopie-pentomino.
Er zijn in totaal
12 oplossingen.
Een ander idee is de twee horizontale randen of de twee verticale randen
samen te plakken zodat je een cilinder bekomt.
Als we de verticale randen samen plakken zijn er 12 oplossingen.
Als we de horizontale randen samen
plakken zijn er 22 oplossingen.
Hieronder vind je er van elke soort een voorgesteld.
|
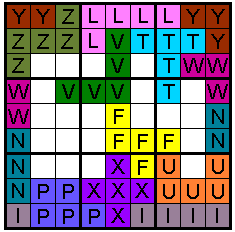
verticale randen samen plakken |
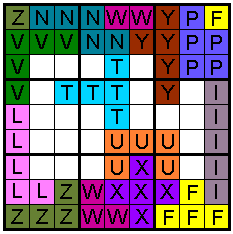
horizontale randen samen plakken |
Voegen we horizontale en verticale randen samen dan zijn er 6577 oplossingen
(34 cilinders inbegrepen).
Helmut stuurde ons
een tekstbestand met alle oplossingen en uitleg.
Het tweede voorbeeld hierboven is oplossing 337 met als uitleg "337 V.......V..V
3V 0H 0B 3A"
337 is het nummer van de oplossing, dan volgen in volgorde van de
alfabetische rangschikking van de pentomino's 12 tekens: "V" voor F-pento ,
W-pento en Z-pento en "." voor de rest, dat wil zeggen dat F-pento, W-pento
en Z-pento over de rand gaat en de andere niet.
Grote
getallen in sudoku's
In de volgende sudoku's komen geen pentomino's
voor maar er moet flink nagedacht worden. Deze sudoku's kunnen gebruikt
worden ter gelegenheid van één of ander feest.
Goede oplossers verwerven eeuwige roem, door vermelding van hun naam bij de
opgeloste sudoku.
Mail naar:
OdetteDM@outlook.com
|
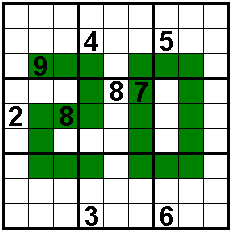
Som getallen in de zeven groepjes van drie is 15.
In de twee verticale groepjes van vijf zijn de cijfers oplopend dan
wel aflopend.
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Ilse De Boeck - België
Nico Looije - Nederland - tijd: 0,016 s
Martin Friedeman - Nederland
Sander Waalboer - Nederland start=16:13:59 16-10-2016
oplossing= 16:14:00
Aad Thoen - Nederland
George Sicherman - USA |
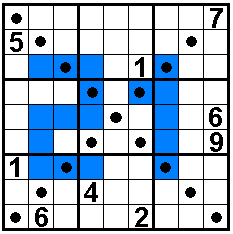
De gestipte vakken bevatten ook 1 tot en met 9.
In de gekleurde vakjes staan oneven getallen.
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Nico Looije - Nederland - tijd: 0,031 s
Martin Friedeman - Nederland
Sander Waalboer - Nederland
start=18:09:38 16-10-2016
oplossing=18:09:44
Ilse De Boeck - België
Aad Thoen - Nederland
Bob Henderson - USA
George Sicherman - USA |
|
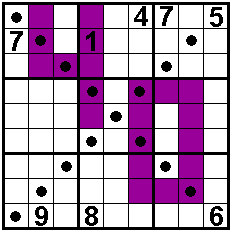
De twee gestipte diagonalen bevatten ook 1 tot en
met 9.
In de gekleurde vakjes staan oneven getallen.
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Nico Looije - Nederland - tijd: 0,046 s
Martin Friedeman - Nederland
Sander Waalboer - Nederland
start=18:17:53 16-10-2016
oplossing=18:18:13
Aad Thoen - Nederland
Bob Henderson - USA
"Wat een fantastische puzzel vanwege de zgn. clusters"
George Sicherman - USA |
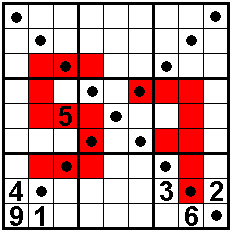
De gestipte vakken bevatten ook 1 tot en met 9.
In de gekleurde vakjes staan oneven getallen.
Diagonale buren zijn ongelijk.
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Nico Looije - Nederland - tijd: 0,218 s
Martin Friedeman - Nederland
Sander Waalboer - Nederland start=18:29:58
16-10-2016
oplossing=18:30:18
George Sicherman - USA
Aad Thoen - Nederland |
|
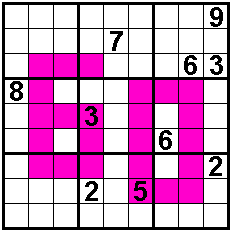
Getallen in de gekleurde vakjes zijn oneven.
Diagonale buren zijn ongelijk.
Tien hints.
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Nico Looije - Nederland - tijd: 0,047 s
Martin Friedeman - Nederland
Sander Waalboer - Nederland start=18:54:48
16-10-2016
oplossing= 18:56:13
George Sicherman - USA
Aad Thoen - Nederland |
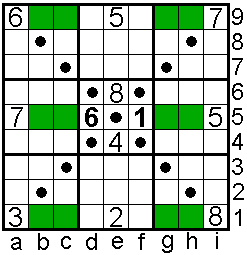
De gestipte vakken bevatten ook 1 tot en met 9.
Diagonale buren zijn ongelijk.
b9c9-g9h9 = 61
b5c5-g5h5=61
b1c1-g1h1=61
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Martin Friedeman - Nederland
Sander Waalboer - Nederland start=19:10:42
16-10-2016
oplossing=19:10:45
Nico Looije - Nederland - tijd: 0,016 s
Aad Thoen - Nederland |
|
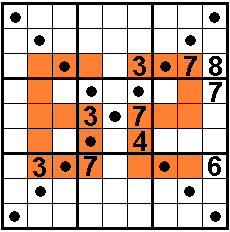
De gestipte vakken bevatten ook 1 tot en met 9.
Getallen in gekleurde series van drie op- dan wel
aflopend. Geldt ook voor de verticale serie van vijf.
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Nico Looije - Nederland - tijd: 0,016 s
Martin Friedeman - Nederland
Sander Waalboer - Nederland start=19:18:52
16-10-2016
oplossing=19:18:53
George Sicherman - USA
Aad Thoen - Nederland |
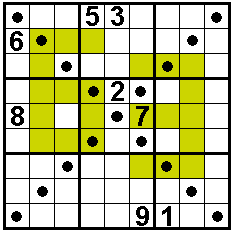
De gestipte vakken bevatten ook 1 tot en met 9.
In de gekleurde vakjes staan oneven getallen.
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Nico Looije - Nederland - tijd: 0,078 s
Martin Friedeman - Nederland
Sander Waalboer - Nederland start=19:24:06
16-10-2016
oplossing=19:24:07
Bob Henderson - USA
Aad Thoen - Nederland |
|
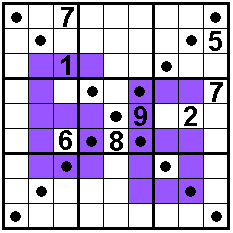
De gestipte vakken bevatten ook 1 tot en met 9.
In de gekleurde vakjes staan oneven getallen
.
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Nico Looije - Nederland - tijd: 0,078 s
Martin Friedeman - Nederland
Sander Waalboer - Nederland start=19:33:28
16-10-2016
oplossing=19:33:41
Bob Henderson - USA
George Sicherman - USA
Aad Thoen - Nederland |
Ontvangen van Aad van de Wetering op 10 oktober 2017
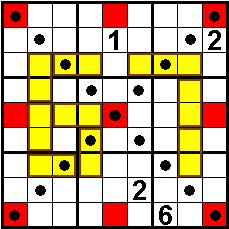
De gestipte vakken bevatten ook 1 tot en met 9,net als de rode
vakjes.
Elke gele domino/tromino bevat een priemgetal
(gelezen van links naar rechts, dan wel van boven naar beneden).
De rode vakjes vormen een magisch vierkant.
.
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Aad Thoen - Nederland
Sander Waalboer - Nederland
Martin Friedeman - Nederland
Nico Looije - Nederland |
|
Ontvangen van Aad van de
Wetering op 10 oktober 2018
Aad mailde:"Bijgevoegd een speciaal voor jou
gecomponeerde sudoku met niet toevallig 10 hints. De 6 en de 8
zitten er natuurlijk bij, je zult ze nog wel meer zien tijdens het
oplossen."
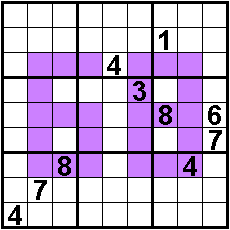
Gekleurde vakjes
3x verticaal : de som van de vijf cijfers is 25
1x verticaal : de som van de drie cijfers is 15
6x horizontaal : de som van de drie cijfers is 15
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Martin Friedeman - Nederland
Nico Looije - Nederland
George Sicherman - USA
Sander Waalboer - Nederland
Aad Thoen - Nederland |
Ontvangen van Aad van de
Wetering op 10 oktober 2019
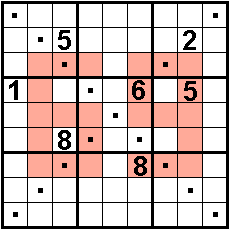
Diagonale buren zijn ongelijk.
In de twee hoofddiagonalen ook 1 t/m 9.
In drie of vijf aaneengesloten gekleurde vakjes zijn de cijfers
ofwel oplopend ofwel aflopend.
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Nico Looije - Nederland
Martin Friedeman - Nederland
George Sicherman - USA
Aad Thoen - Nederland
Sander Waalboer - Nederland |
In januari 2020 kregen we van Aad van de Wetering twee schitterende sudoku "83".
Op 16 januari 2020 kregen we van Martin Kindt een bericht "Toevallig ben ik vandaag een priemgetal geworden, een waarvan de som van de cijfers ook een priemgetal is en waarvan zelfs de
som van de cijfers van de som van de cijfers ook priem is. Dat is sinds ik in de dubbele cijfers kwam twee keer eerder gebeurd".
We dragen de volgende sudoku's aan hem op.
Martin Friedeman "Dat was zeker genieten geblazen!"
|
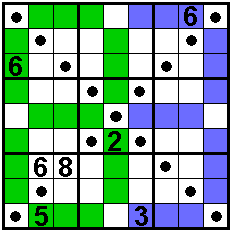
Som drie gekleurde vakjes steeds 15
Ook diagonalen 1 t/m 9
Oplossers: Aad van de Wetering - Nederland
Aad Thoen - Nederland
Odette De Meulemeester - België
Nico Looije - Nederland
Martin Friedeman - Nederland
Sander Waalboer - Nederland
George Sicherman - USA |
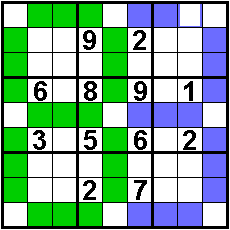
Som drie gekleurde vakjes steeds 18
Oplossers: Aad van de Wetering - Nederland
Aad Thoen - Nederland
Odette De Meulemeester - België
Nico Looije - Nederland
Martin Friedeman - Nederland
Sander Waalboer - Nederland
George Sicherman - USA |
Ontvangen van Aad van de Wetering voor het nieuwe jaar
2020. Veel plezier ermee!
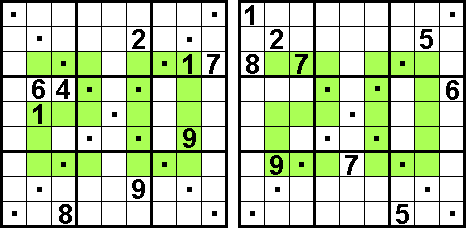
In de twee hoofddiagonalen ook 1 t/m 9.
Som van drie aaneengesloten groene vakjes is 15.
Som van vijf aaneengesloten groene vakjes is 25.
Oplossers: Aad van de Wetering - Nederland
Aad Thoen - Nederland
Odette De Meulemeester - België
Matthijs Coster - Nederland
Martin Friedeman - Nederland
Nico Looije - Nederland
Sander Waalboer - Nederland
George Sicherman - USA
We kunnen het niet laten om te melden dat 2020 een
autobiografisch getal is.
We hopen dat we ook een sudoku krijgen op 5 mei.
In het schitterend boekje
"Exotische sudoku's" van Aad Thoen en Aad van de Wetering staan er nog
heel wat: 19, 24, 32, 37,44, 50, 52, 64, 66, 69, 83 en 88.

Je kan het o.a. bestellen bij
Standaard Boekhandel.
Op 13 maart 2019 kreeg ik van Aad Thoen zijn schitterend
boek "Sudoku Patterns"
Was dit voor mijn Pi-dag?
Een boek over patronen in de voltooide sudoku en zijn vele aspecten:
symmetrie, trio's, diagonalen, verschuivingen, magie en nog veel meer
fantasievolle dingen.

Om iemand in het zonnetje te zetten zijn hier nog twee sudoku's van de hand
van Aad van de Wetering.
|

De som van de getallen in elk van de acht trio's is
gelijk aan 15.
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Nico Looije - Nederland - tijd: 0,593 s
Martin Friedeman - Nederland
George Sicherman - USA
Sander Waalboer - Nederland
start=08:40:01 17-10-2016
oplossing=08:40:02
Bob Henderson - USA
Aad Thoen - Nederland |
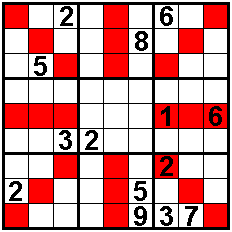
De som van de getallen in elk van de acht trio's is
gelijk aan 15.
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Nico Looije - Nederland - tijd: 0,063 s
Martin Friedeman - Nederland
Sander Waalboer - Nederland start=08:40:23 17-10-2016
oplossing=08:40:27
George Sicherman - USA
Bob Henderson - USA
Aad Thoen - Nederland |
Tijdens Corona-tijden (2020) stuurde Bob Henderson ons twee
bloemen-sudoku's toe.
|
Summer Sunflower Sudoku

"The orange cells must contain odd digits, the yellow cells must
contain even digits, and the brown cells must contain a magic
square, so that the 3 digits in each row, column, and diagonal add
to 15. The solution is unique except that columns 4 and 6 may be
interchanged (the clues in the brown area allow only 2 orientations
of the magic square from among the 8 possible orientations, some of
which would result in multiple Sudoku solutions)"
Oranje vakken: oneven cijfers
Gele vakjes: even cijfers
Midden vak: magisch vierkant van 3x3
Er zijn 2 oplossingen waarbij de vierde en zesde kolom verwisselbaar
zijn. Sommige van onze vrienden vinden dat een sudoku maar juist één
oplossing mag hebben. Dit kan je voorkomen door een hint toe te
voegen in bijvoorbeeld de vierde kolom.
Oplossers: Bob Henderson - USA
Martin Friedeman - Nederland
Odette De Meulemeester - België
Aad van de Wetering - Nederland
Nico Looije - Nederland
Helmut Postl - Oostenrijk
George Sicherman - USA |
Zonnehoed Sudoku (Coneflower)
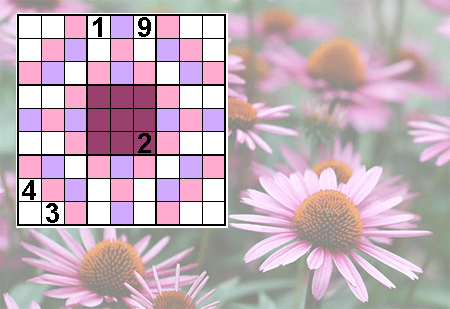
"Each diagonal must contain the
digits 1 - 9. The purple cells hold even digits, the
pink cells hold odd digits, and the darker central area must make a
3x3 magic square. The clues make it easy to fill in that part, but
then there very few more to help you fill in the rest! If you need
help with this Sudoku I can send you more clues. . ."
Paarse vakjes: even cijfers
Roze vakjes: oneven cijfers
Midden vak: magisch
vierkant van 3x3
Ook diagonalen bevatten cijfers 1 t/m 9
Oplossers: Bob Henderson - USA
Odette De Meulemeester - België
Aad van de Wetering - Nederland
Martin Friedeman - Nederland
Nico Looije - Nederland
"deze oplossing liet
zich niet echt beredeneren"
|
Voor "65" maakte Aad deze pento-sudoku
met 65 vakjes
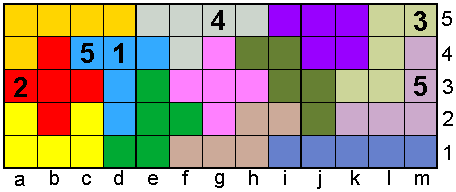
Drie 5x5 geschakelde sudoku's a1-e5, e1-i5, i1-m5
Elke pentomino bevat ook de cijfers 1 tot en met 5
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Nico Looije - Nederland - tijd: 0,016 s
Martin Friedeman - Nederland
Bob Henderson - USA
George Sicherman - USA
Aad Thoen - Nederland
Matthijs Coster - Nederland
Voor "69" maakte Helmut Postl de volgende bijzondere tekening.

De volgende vorm heeft een unieke oplossing met de pentomino's.
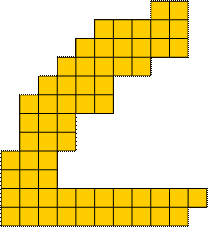
Neem telkens twee kopies van de vorm, draai één van deze en voeg ze samen om een
6 en een 9 te maken:
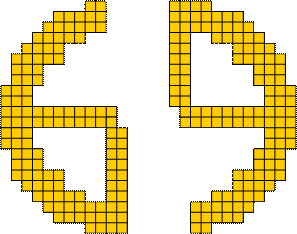
Voeg deze nu samen tot de eerste figuur.
En de oplossing:

Voor "73" vertelde Helmut Postl
73 is an extraordinary number:
73 is the 21st prime, and the mirror number 37 is the 12th prime, that is
the mirror number of 21. Moreover, 21=7*3. Numbers like this one are called
Sheldon numbers after the character Sheldon in the TV series The Big Bang
Theory, that is: If p is the n-th prime, then mirror(p) is the mirror(n)-th
prime, and furthermore, n is the product of the digits of p. It is proven
that 73 is the only Sheldon number.
There are a lot of palindromes in the binary representation:73 = 1001001; 21
= 10101; 7 = 111; 3 = 11
The binary representation of 73 has 7 digits of which 3 are ones.
And the representation in the octal system is also a palindrome: 73 = 111.
And one more palindrome: In Morse Code, 73 is - - . . . . . . - -
The number of days in a normal year is just five times 73.
The 73rd day in a normal year is Pi Day.
Hij maakte ook een
speciale vorm van de letter 'O' met juist
73 pentomino-oplossingen!
Voor de 51ste dag van de wiskunde aan de KULAK maakte Aad van de Wetering
voor ons 2 sudoku's: een moeilijke en een makkelijker (alhoewel?)
|
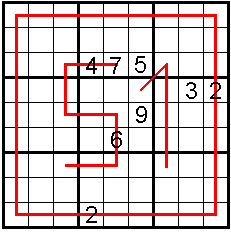
Buurcijfers in een rode lijn hebben als grootste gemene deler 1.
Cijfers op paardensprongafstand zijn nooit gelijk.
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Martin Friedeman - Nederland
Nico Looije - Nederland
Aad Thoen - Nederland
"Niet triviaal maar was goed te doen, vooral
door de speciale rol van de 6."
Sander Waalboer - Nederland
George Sicherman - USA |
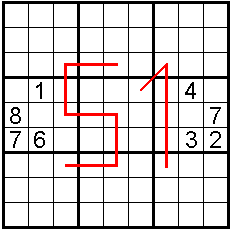
Buurcijfers in
een rode lijn verschillen minstens 5.
Cijfers op paardensprongafstand zijn nooit gelijk.
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Nico Looije - Nederland
Martin Friedeman - Nederland
Aad Thoen - Nederland
George Sicherman - USA
Sander Waalboer - Nederland |