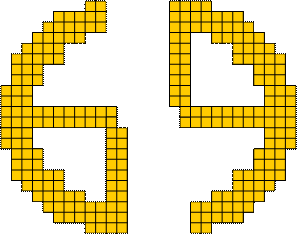Numbers with unique solutions of Helmut Postl
Large
numbers in Sudoku and pentominos
We asked Helmut if he could think of something fun
with "70" (for the anniversary of Aad van de Wetering November 16, 2014) and
we got a wonderful sudoku connected with a lot pentominoproblems.
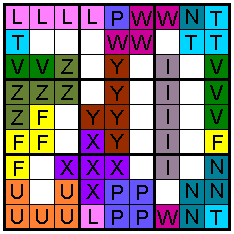
The following Sudoku has the additional property that the values in all
coloured cells sum up to 70.
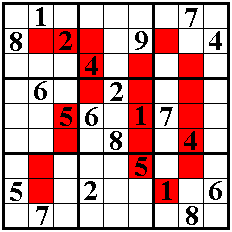
Correct solutions earn eternal fame.
Send your solution to:
o.d.m@fulladsl.be
| Name |
Country |
| Helmut Postl |
Austria |
| Aad Thoen |
The Netherlands |
| Aad van de Wetering |
The Netherlands |
| Odette De Meulemeester |
Belgium |
| Sander Waalboer |
The Netherlands |
| George Sicherman |
USA |
| Nico Looije |
The Netherlands |
| Bob Henderson |
USA |
| Matthijs Coster |
The Netherlands |
| Peter Jeuken |
The Netherlands |
George Sicherman:"I solved them by computer. Doing it by hand would take
too much trial and error, and I already have enough trial and error in my
life!"
Bob Henderson: "I found the following results by modifying my Sudoku
solver to run until the marked cells had the correct sums. I did not search
for any more solutions: I have no doubt that Helmut designed them to have
only one!"
Furthermore, there are 60 white cells, so they can be
covered by 12 pentominoes. Unfortunately, it is not possible to use each
pentomino exactly once.
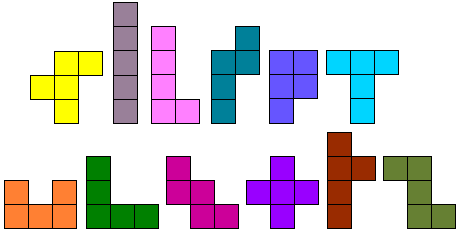
But there are some interesting possibilities:
1)Choose 4 pentominoes and use each one three times. The choice is unique,
and there are
two trivially connected solutions.
2) The biggest number of different pentominoes used is 9.
There are several possibilities. One among them is unique: it is without the
N pentomino.
Here is the solution.
3)The smallest number of pentominoes used is 3. Each of
them can be used in an arbitrary number of copies.
The solution is unique.
4) The biggest number of copies of a single pentomino is 8. The remaining 4
pieces need not be different. There are two trivially connected solutions.
Another idea is to glue the two horizontal edges together so to make a
cylinder. Unfortunately, there are still no solutions. The same holds when
the two vertical edges are glued together. But combining both (so to make a
torus) yields 105 solutions. There are two unique ones among them: one with
the fewest (4) and one with the most (9) pentominoes wrapping around.
|
one with the fewest (4) pentominoes wrapping around |
one with the most (9) pentominoes wrapping around |
Helmut send a
text file with all the solutions.
Let W = number of wrapped pentominoes, S = number of solutions for this
case. Then we have the following possibilities:
(W,S) = (4,5), (5,14), (6,33), (7,42), (8,10), (9,1).
You can find the solutions as above: Search for “4A” resp. “9A” to get the
solutions with the fewest resp. most wrapping pentominoes.
Helmut made a similiar
for 64. (October 10, 2014)
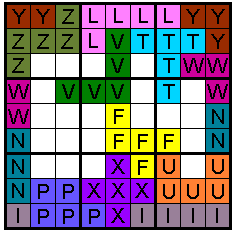
The following Sudoku has the additional property that the values in all
coloured cells sum up to 64.
Correct solutions earn eternal fame.
Send your solution to:
o.d.m@fulladsl.be
| Name |
Country |
| Helmut Postl |
Austria |
| Aad Thoen |
The Netherlands |
| Aad van de Wetering |
The Netherlands |
| Odette De Meulemeester |
Belgium |
| Sander Waalboer |
The Netherlands |
| George Sicherman |
USA |
| Nico Looije |
The Netherlands |
| Bob Henderson |
USA |
| Martin Friedeman |
The Netherlands |
| Peter Jeuken |
The Netherlands |
Aad van de Wetering: "Voor de
64 (ook een idee) had ik geen software, met Xudoku alle oplossingen gemaakt
en Excel laten uitrekenen welke som 64 had voor de gevraagde vakjes. Dat was
er één, alle andere hadden een grotere som."
Sander Waalboer zal daar wel software voor hebben want op 10 min stuurde
hij zowel een oplossing voor "64" als voor "70" terug
Nico Looije: "Dit is een leuk idee. Ik moest een minimale programmatische
aanpassing doen om ze op te lossen"
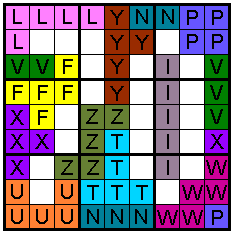
Furthermore, there are 60 white cells (ignoring the isolated cell in the
digit 6), so they can be covered by 12 pentominoes. Unfortunately, it is not
possible to use each pentomino exactly once.
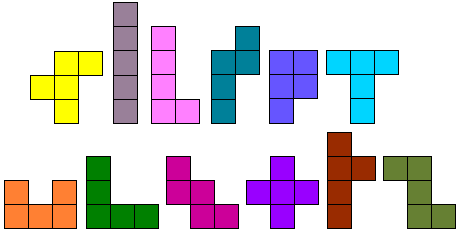
But there are some interesting possibilities:
1)Choose 6 pentominoes and use each one twice. There are many
possibilities. Try a set without the L or the P pentomino.
Without the L-pentomino: 2
combinations.
INPTWY: 3
solutions
INPUVY: 1
solution
Without the P-pentomino : 2 combinations.
ILNTVY: 2 solutions
ILNTVW: 1 solution
2) Choose 4 pentominoes and use each one three times. The choice is unique,
and there are
three trivially connected solutions .
3)The biggest number of different pentominoes used is 10. There are many
possibilities. Three among them are unique:
one without the L pentomino
one without the N
one with the X
4) The smallest number of pentominoes used is 4. There are many
possibilities.:
One among them is unique: it uses the Z pentomino.
5)The biggest number of copies of a single pentomino is 8. The remaining 4
pieces need not be different. There are three essentially different
possibilities, but all with the same 8 copy pentomino.
There are
12 solutions.
Another idea is to glue the two horizontal and/or vertical edges together so
to make a cylinder or a torus.
W = number of wrapped pentominoes, S =
number of solutions for the corresponding case.
1) Connect the vertical edges (vertical cylinder): There are 22 solutions.
(W,S) = (2,3), (3,10), (4,7), (5,2).
2) Connect the horizontal edges (horizontal cylinder): There are 12
solutions.
(W,S) = (3,3), (4,9).
3) Connect the horizontal and vertical edges (torus): There are
6577 solutions (including the 34 cylinders).
(W,S) = (2,16), (3,179), (4,852), (5,2029), (6,1926), (7,1087), (8,434),
(9,51), (10,3).
|
vertical cylinder |
horizontal cylinder |
Helmut added the wrap information to
the first line of each solution. Here is an example: "2768 HVH.H.V.BB.. 4V
5H 2B 7A"
2768 is the solution number.
The next string consists of 12 characters, one for each pentomino in
alphabetical order (FILNPTUVWXYZ).
‘V’ = only vertical wrap, ‘H’ = only horizontal wrap, ‘B’ = both wraps, ‘.’
= no wrap.
The following four numbers are the numbers of pentominoes with the indicated
wrap kind: ‘V’ = vertical, ‘H’ = horizontal, ‘B’ = both, ‘A’ = any. V
includes also B (since a pentomino with both wraps does also wrap
vertically), H includes also B (for the same reason), and A can be computed
as A = V + H – B.
The given example means that I and U wrap only vertically, F, L and P wrap
only horizontally, and W and X wrap in both ways. There are 4 pentominoes
that wrap vertically (IUWX), 5 horizontally (FLPWX), 2 in both ways (WX) and
7 anyway (FILPUWX).
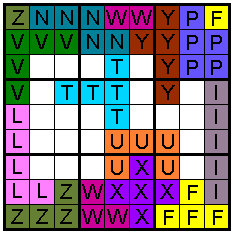
Large numbers in Sudoku
The following sudoku puzzles are
not with pentominos but they are funny. The Sudoku can be used at one or
other occasion.
Correct solutions earn eternal fame.
Send your solution to:
o.d.m@fulladsl.be
|
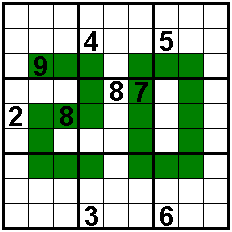
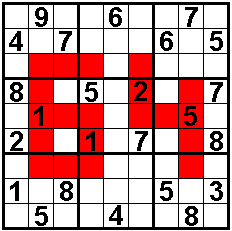
The sum of the
numbers in the seven horizontal or
vertical I-trominoes (three cells) is 15.
In the two vertical I-pentomino (five
cells) are the numbers form an increasing or decreasing sequence.
Solvers: Aad van de Wetering - The Netherlands
Odette De Meulemeester - Belgium
Nico Looije - The Netherlands
Martin Friedeman - The Netherlands
Ilse De Boeck - Belgium
Sander Waalboer - The Netherlands
Aad Thoen - The Netherlands
George Sicherman - USA |
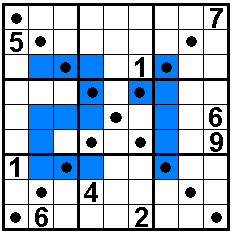
The
diagonals also contain 1 to 9.
In the colored cells are odd
numbers
Solvers:
Aad van de Wetering - The Netherlands
Odette De Meulemeester - Belgium
Nico Looije - The Netherlands
Martin Friedeman - The Netherlands
Sander Waalboer - The Netherlands
Ilse De Boeck - Belgium
Aad Thoen - The Netherlands
Bob Henderson - USA
George Sicherman - USA |
|
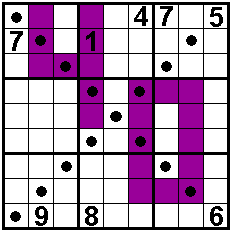
The
diagonals also contain 1 to 9.
In the colored cells are odd
numbers
Solvers: Aad van de Wetering - The
Netherlands
Odette De Meulemeester - Belgium
Nico Looije - The Netherlands
Martin Friedeman - The Netherlands
Sander Waalboer - The Netherlands
Aad Thoen - The Netherlands
Bob Henderson - USA
George Sicherman - USA |
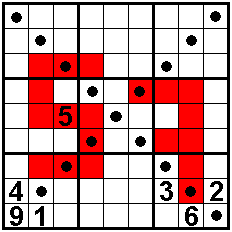
The
diagonals also contain 1 to 9.
In the colored cells are odd
numbers
Direct diagonal neighbours are
different.
Solvers: Aad van de Wetering - The
Netherlands
Odette De Meulemeester - Belgium
Nico Looije - The Netherlands
Martin Friedeman - The Netherlands
Sander Waalboer - The Netherlands
Aad Thoen - The Netherlands
George Sicherman - USA |
|
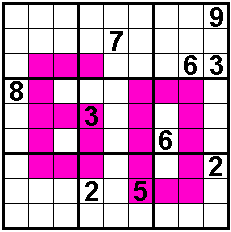
In the
colored cells are odd numbers
Direct diagonal neighbours are
different..
Ten hints.
Solvers: Aad van de Wetering - The
Netherlands
Odette De Meulemeester - Belgium
Nico Looije - The Netherlands
Martin Friedeman - The Netherlands
Sander Waalboer - The Netherlands
George Sicherman - USA
Aad Thoen - The Netherlands |
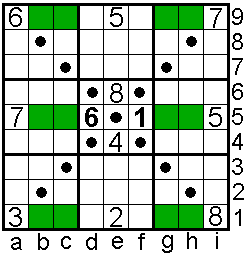
The
diagonals also contain 1 to 9.
Direct diagonal
neighbours are different.
b9c9-g9h9 = 61
b5c5-g5h5=61
b1c1-g1h1=61
Solvers: Aad van de Wetering - The
Netherlands
Odette De Meulemeester - Belgium
Martin Friedeman - The Netherlands
Sander Waalboer - The Netherlands
Nico Looije - The Netherlands
Aad Thoen - The Netherlands |
|
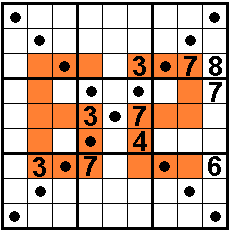
The
diagonals also contain 1 to 9
In the vertical I-pentomino (five
cells) are the numbers form an increasing or decreasing sequence.
Also in the night horizontal or vertical I-trominoes (three
cells) are the numbers form an increasing or decreasing sequence.
Solvers: Aad van de Wetering - The Netherlands
Odette De Meulemeester - Belgium
Nico Looije - The Netherlands
Martin Friedeman - The Netherlands
Sander Waalboer - The Netherlands
George Sicherman - USA
Aad Thoen - The Netherlands |
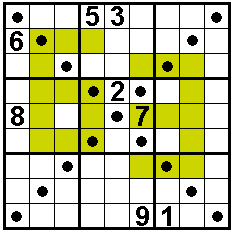
The
diagonals also contain 1 to 9
In the
colored cells are odd numbers
Solvers: Aad van de Wetering - The Netherlands
Odette De Meulemeester - Belgium
Nico Looije - The Netherlands
Martin Friedeman - The Netherlands
Sander Waalboer - The Netherlands
Bob Henderson - USA
Aad Thoen - The Netherlands |
|
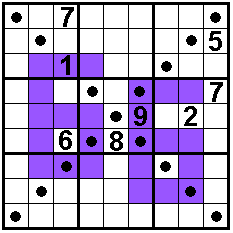
The
diagonals also contain 1 to 9
In the
colored cells are odd numbers
Solvers: Aad van de Wetering - The
Netherlands
Odette De Meulemeester - Belgium
Nico Looije - The Netherlands
Martin Friedeman - The Netherlands
Sander Waalboer - The Netherlands
Bob Henderson - USA
George Sicherman - USA
Aad Thoen - The Netherlands |
Recieve of Aad van de Wetering on octobre
10,
2017
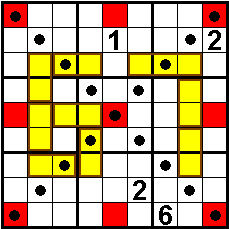
The
diagonals also contain 1 to 9,
just like the red squares.
Each yellow domino / tromino contains a prime number
(read from left to right, or from top to bottom).
The red squares form a magic square.
.
Solvers: Aad van de Wetering -
The Netherlands
Odette De Meulemeester -
Belgium
Aad Thoen - The Netherlands
Sander Waalboer - The Netherlands
Martin Friedeman - The Netherlands
Nico Looije - The Netherlands |
|
Recieve of Aad van de Wetering on octobre 10, 2018
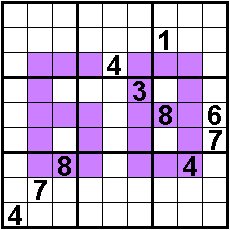
In the colored cells
3x vertical : the sum
of the 5
numbers is 25
1x vertical :
the sum of the
3 numbers is 15
6x horizontal : the sum
of the 3
numbers is 15
..
Solvers: Aad van de Wetering - The Netherlands
Odette De Meulemeester - Belgium
Sander Waalboer - The Netherlands
Martin Friedeman - The Netherlands
Nico Looije - The Netherlands
George Sicherman - USA
Aad Thoen - The Netherlands |
Recieve of Aad van de Wetering on octobre
10, 2019
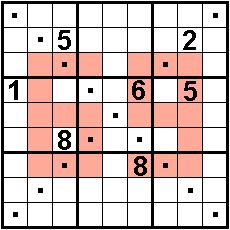
Direct diagonal
neighbours are different. .
The
diagonals also contain 1 to 9
In the vertical I-pentominoes (five
cells) are the numbers form an increasing or decreasing sequence.
Also in the eight horizontal or vertical I-trominoes (three
cells) are the numbers form an increasing or decreasing sequence.
Oplossers: Aad van de Wetering - Nederland
Odette De Meulemeester - België
Nico Looije - Nederland
Martin Friedeman - Nederland
George Sicherman - USA
Aad Thoen - The Netherlands |
In the splendid book "Exotische
sudoku's" by Aad Thoen and Aad van de Wetering is more: 19, 24, 32, 37,44, 50, 52, 64, 66, 69, 83
and 88.

You can order this book e.g. at Standaard Boekhandel.

Here are two
sudoku puzzles written by Aad van de Wetering to put someone in the
spotlight .
|

The sum of the numbers in each of the
eight trios is equal to 15.
Solvers: Aad van de Wetering - The
Netherlands
Odette De Meulemeester - Belgium
Martin Friedeman - The Netherlands
Nico Looije - The Netherlands
George Sicherman - USA
Sander Waalboer - The Netherlands
Bob Henderson - USA
Aad Thoen - The Netherlands |
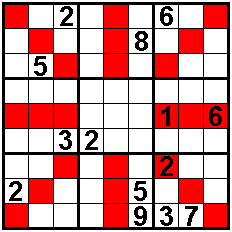
The sum of
the numbers in each of the eight trios is equal to 15.
Solvers: Aad van de Wetering - The Netherlands
Odette De Meulemeester - Belgium
Martin Friedeman - The Netherlands
Nico Looije - The Netherlands
Sander Waalboer - The Netherlands
George Sicherman - USA
Bob Henderson - USA
Aad Thoen - The Netherlands |
For "65"
Aad made this pento sudoku with 65
cells.
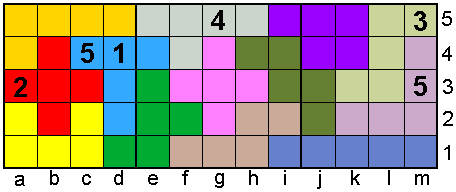
Three 5x5 concatenated sudoku's a1-e5, e1-i5, i1-m5
Each pentomino must have the numbers 1, 2,3,4 and 5
Solvers: Aad van de Wetering - The Netherlands
Odette De Meulemeester - Belgium
Martin Friedeman - The Netherlands
Nico Looije - The Netherlands
Bob Henderson - USA
George Sicherman - USA
Aad Thoen - The Netherlands
We got a very special mail:
I wish you all the best for your
 -th
birthday!
-th
birthday!
This is my special number design for your birthday!
The following pattern has a unique solution with the pentominoes
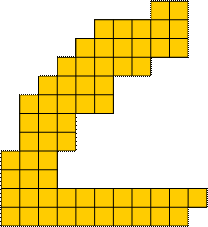
Take two copies of the pattern, rotate one of them, and put them together to
build the digit 6 resp. 9:
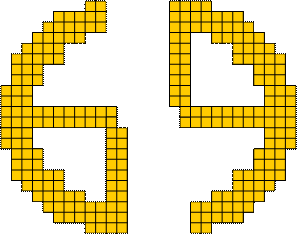
And then put them together to build the design from above.
The solution:


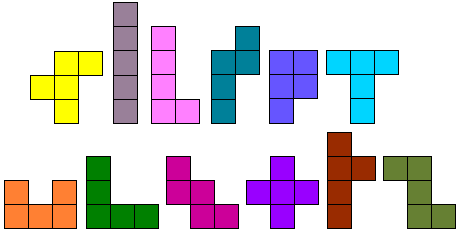



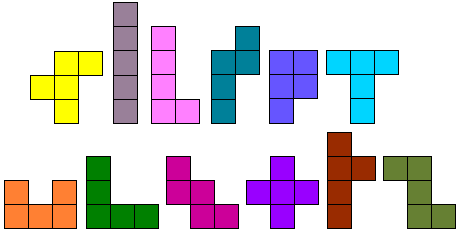



















 -th
birthday!
-th
birthday!