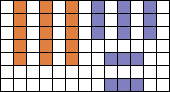
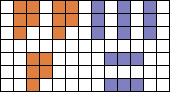
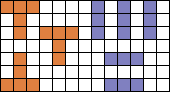
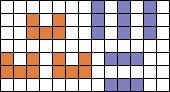
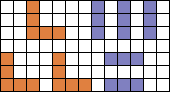
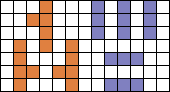
5 I-tromino's en 3 pentomino's in congruente figuur

We kregen een mail van Aad van de Wetering waarbij hij vertelde dat op www.mathpuzzle.com het volgende stond: Patrick Hamlyn:"Robert Reid sent me a very nice little manual puzzle which took several attempts over a week or two before I got it. Using cardboard, plastic, neoprene, high-density foam, icecream container lid or just paper: Cut out five straight trominos and three U-pentominos in the same scale. Now cover one set with the other. Real easy right? Everyone I've given it to swears blind it's impossible. Some get it in a few minutes, many (like me) take days or weeks. Here I reproduce Robert's 'spiel': COVER - UP: As usual the politicians have buundered; they are trying to cover-up three twisted facts by five straight lies and they are getting nowhere. Can you show them how it is done? There is only one solution. " [I got a copy of this as well -- it's a fantastic little puzzle.]
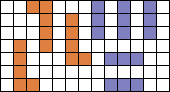
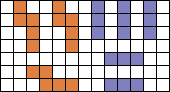
Aad schreef verder "Oftewel: bedek 3 U-pentomino's met 5 I-tromino's. Lastig, maar ik heb de oplossing net zelf gevonden. Eerst denk je dat het onmogelijk is, maar dat is niet zo. Heel fraai! "

We probeerden dit ook voor de andere pentomino's.Voor F,W, X en Z vonden we geen oplossing.