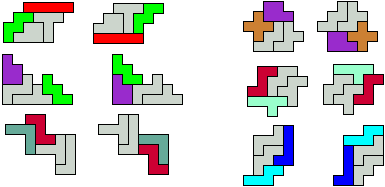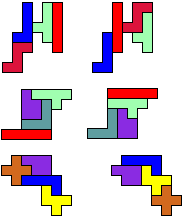3
(of meer) verschoven pentomino's in congruente vormen.
| Dit leuke probleem kregen we van Aad Thoen |
|
Beschouw volgende twee figuren.

Merk op dat ze congruent zijn en beide
dezelfde drie hexomino's bevatten die ten opzichte van elkaar verschoven zijn.
Opgave: doe hetzelfde met drie pentomino's.
We kregen Van Aad Thoen een mooi document met uitleg over een methode voor het
construeren van congruente figuren bestaande uit verschoven pentomino's
Wil je het document zien? Druk dan
hier.
Helmut stuurde volgende mail:"Here is a complete list of all 3-patterns. (I
checked them twice, so they should be ok...)"
Er zijn 78 oplossingen en 77 verschillende vormen (er is één vorm die met
twee verschillende combinaties van drie verschillende pentomino's kan gevuld
worden)
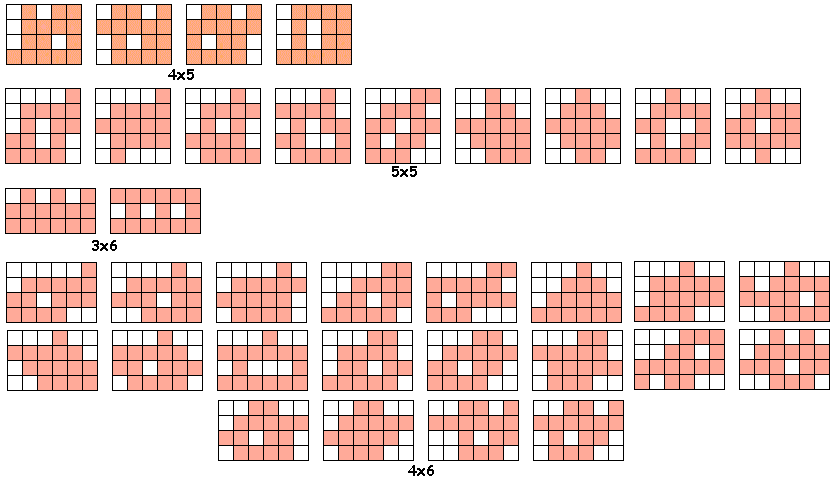
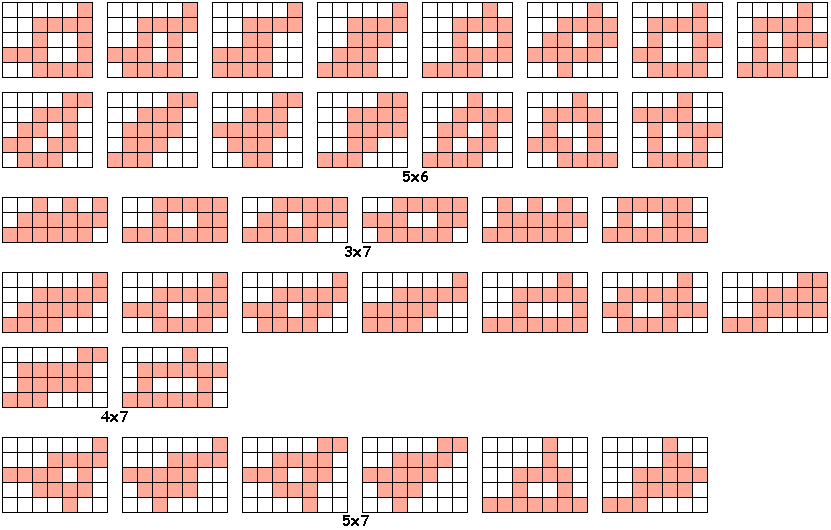
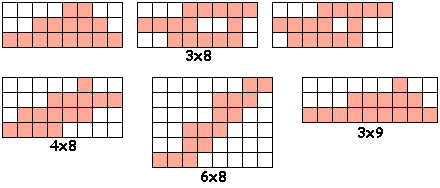
Wil je de
oplossingen zien gevuld met pentomino's ?
We kregen van Helmut een volgende mail:
"Regarding your record pattern with 9 pentominoes I tried to achieve more.
Then I had the idea to simply take a pattern of area 60, to fill it with the
pentos and to look after solutions where the pentos are only translated. The
first pattern I tried was the 6x10 rectangle which has 2339 solutions in total.
I made a table of the orientations of the pentos for each solution, and then I
looked for two identical entries. There are lots, and next I eliminated all
those where there are pentos which do not move. Among the remaining ones, there
are some trivial ones, namely those which are composed of two 5x6 rectangles
where the rectangles simply change place. Again eliminating those trivial ones,
there are exactly two solutions left.
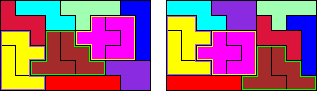
In this solution are some combinations of pentos which move simultaneously,
namely FV, TW and UX.

In this solution there are no such combinations; every pentomino is translated
by a different vector. I like this one.
Next, I tried the 5x12 and 4x15 rectangles.
With the 5x12, there are many with a vertical I-pento and a remaining 5x11
rectangle, and there are some consisting of two smaller rectangles. Omitting
them, there are 8 solutions left and each of them has some combinations of
pentos shifted simultaneously.
|
|
|
The 4x15 rectangle has only
solutions consisting of the two rectangles 4x5 and 4x10.
We zochten zelf ook naar oplossingen gevuld met meer dan 3 pentomino's.
Met 4
pentomino's
Als we 2 congruente decamino's nemen, kunnen we heel veel oplossingen vinden.

|
|
|
Met 5
pentomino's
2 of 3 pentomino's
verplaatsen zich over dezelfde vector.
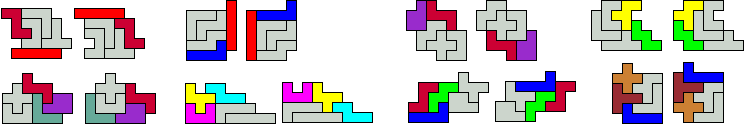
We kunnen deze twee aan twee congruente figuren op heel wat manieren tegen
elkaar leggen tot congruente figuren .

Elke pentomino verschuift over andere
vector.

We kunnen deze twee aan twee congruente figuren op heel wat manieren tegen
elkaar leggen tot congruente figuren .
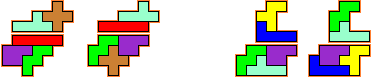
Met 6 pentomino's
Met 2 keer 2 congruente vormen gevuld met 3 pentomino's kunnen we heel wat
oplossingen vinden.

Er zijn ook heel wat oplossingen als we de vorm verdelen in 2 en 4
pentomino's die dan onderling over dezelfde vector verschuiven.
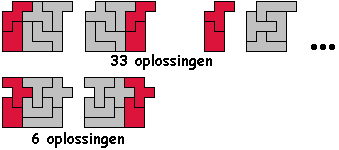
Een paar oplossingen waarbij 3 decamino's die gevuld zijn met 2 pentomino's
verschoven zijn.

Dank zij de methode die Aad Thoen bedacht heeft vonden we nog heel wat
oplossingen.
We maakten hier een afzondelijke pagina voor.
http://pentomino.classy.be/3tdeco3.html
2 of meer
pentomino's verplaatsen zich over dezelfde vector.
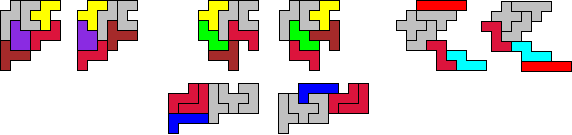
Elke pentomino verschuift over
andere vector.

Met 7
pentomino's
Er zijn heel wat oplossingen als we de vorm
verdelen in 2 en 5 pentomino's of in 3 en 4 pentomino's die dan onderling over
dezelfde vector verschuiven.

Andere triviale oplossingen kan men vinden door de oplossingen met 3 pentomino's
uit te breiden met 2 congruente vormen bestaande uit telkens 2 verschillende
pentomino's.
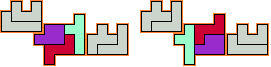
2 of meer pentomino's
verplaatsen zich over dezelfde vector.
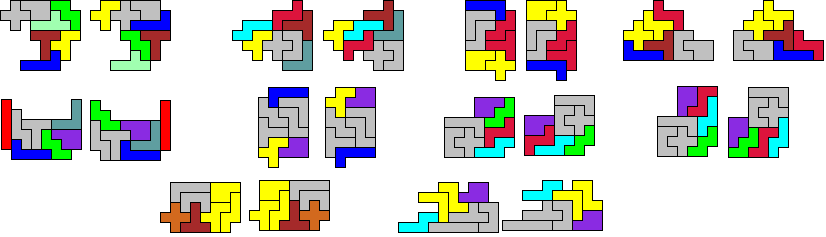
Elke pentomino verschuift over andere
vector.
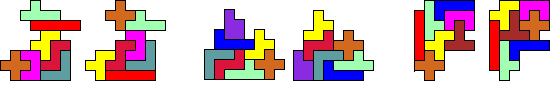
We kunnen deze twee aan
twee congruente figuren op heel wat manieren tegen elkaar leggen tot congruente
figuren .
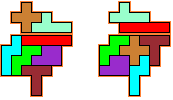
Met 8
pentomino's
Met 2 keer 2 congruente vormen gevuld met 4
pentomino's kunnen we heel wat oplossingen vinden.
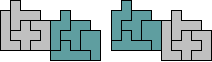
Andere triviale voorbeelden waarbij de vorm in
twee verdeeld wordt en de delen verschoven worden, gaan we niet meer tekenen.
2 of meer pentomino's
verplaatsen zich over dezelfde vector.

Elke pentomino verschuift over andere
vector.
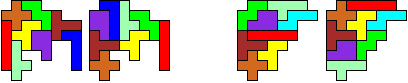
We kunnen deze twee aan
twee congruente figuren op heel wat manieren tegen elkaar leggen tot congruente
figuren .
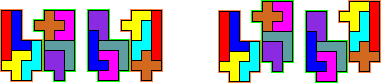
Met 9
pentomino's
Er zijn heel wat triviale oplossingen waarbij
de vorm in twee of drie verdeeld wordt en de delen verschoven worden.
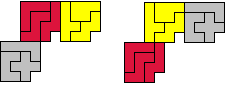
2 of meer pentomino's
verplaatsen zich over dezelfde vector.
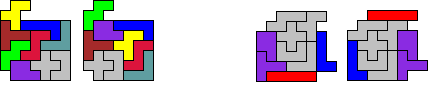
Elke pentomino verschuift over andere
vector.
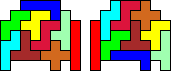
We kunnen deze twee aan
twee congruente figuren op heel wat manieren tegen elkaar leggen tot congruente
figuren .

Met 10 pentomino's
Er zijn heel wat triviale oplossingen waarbij
de vorm in twee (al dan niet congruente) of meer verdeeld wordt en de delen
verschoven worden.
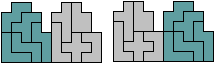
2 of meer pentomino's
verplaatsen zich over dezelfde vector.

Elke pentomino verschuift over andere
vector.
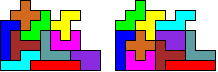
Met 11 pentomino's
Er zijn heel wat triviale oplossingen waarbij
de vorm in twee of meer verdeeld wordt en de delen verschoven worden.
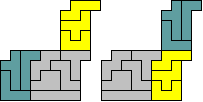
2 of meer pentomino's
verplaatsen zich over dezelfde vector.
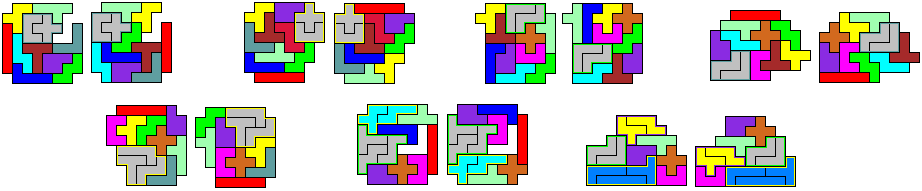
Elke pentomino verschuift over andere
vector.
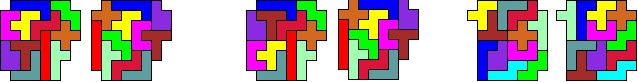
Met 12 pentomino's
Er zijn heel wat triviale oplossingen waarbij
de vorm in twee of meer verdeeld wordt en de delen verschoven worden.

2 of meer pentomino's
verplaatsen zich over dezelfde vector.

Aad Thoen stuurde ons nog een document ter
aanvulling van de vorige.
Je kan het
hier downloaden
Commentaar?
Graag een mail naar:
o.d.m@fulladsl.be