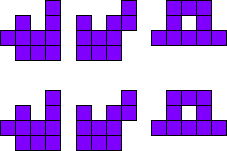
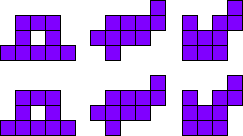
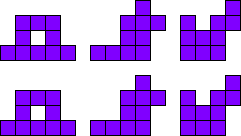
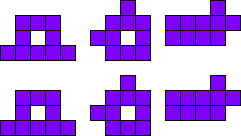
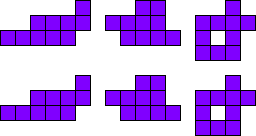
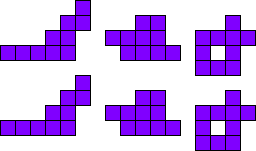
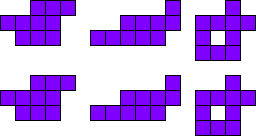
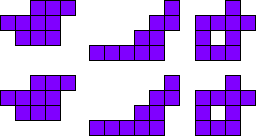
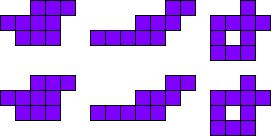
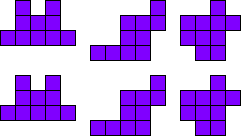
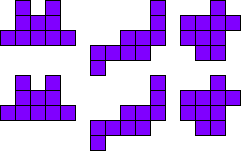
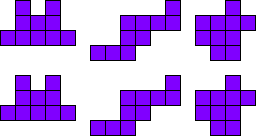
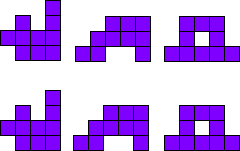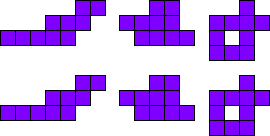3x2 congruente vormen
Dit leuke probleem vonden we op http://home.earthlink.net/~kenzelt/
Leg de pentomino’s per twee.
Maak hiermee 3 maal 2 congruente figuren.

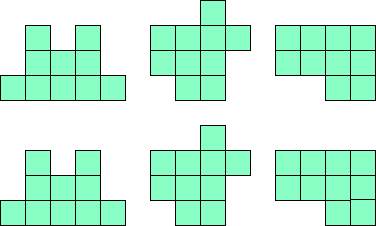
Merk op dat 2 van onze vormen een symmetrie-as hebben.
Een mooie vraag hierbij is: op hoeveel verschillende manieren kunnen we 12 elementen verdelen in 3 groepen van 4?

Kan je nog andere vormen vinden voor dit probleem?
Graag een mail naar:
o.d.m@fulladsl.be

Van Helmut Postl (Wenen) kregen we nog 17 andere oplossingen toegestuurd. We denken dus dat er 18 verschillende oplossingen zijn.
 

FLXY   ITUZ   NPVW	FLXY   ITUZ   NPVW
FLXY   ITUZ   NPVW	FLXY   ITUZ   NPVW
FNVW   ITUZ   LPXY	FPTZ   ILNW   UVXY
FPTZ   ILNW   UVXY	FPTZ   ILNW   UVXY
FPTZ   ILNW   UVXY	FPTZ   ILNW   UVXY
FPTZ   ILNW   UVXY	FITU   LNVZ   PWXY
FITU   LNVZ   PWXY	FITU   LNVZ   PWXY
FNVW   ITUZ   LPXY	FLXY   ITUZ   NPVW

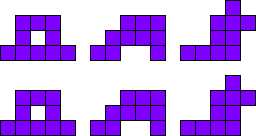
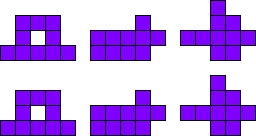
FLXY   ITUZ   NPVW

We bekeken eens welke verdelingen voorkomen:
FITU - LNVZ - PWXY (4)
FLXY - ITUZ - NPVW (6)
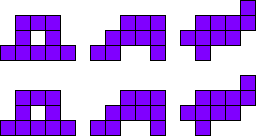
FNVW - ITUZ - LPXY (2)
FPTZ - ILNW - UVXY (6)

Er zijn 165 verschillende groepjes van 4 pentomino's waartoe F behoort en hetzelfde geldt voor de andere pentomino's.
Er zijn maar 4 combinaties waarmee we dit probleem kunnen oplossen (Voor I,T,U en Z zijn er maar 3)