





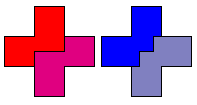
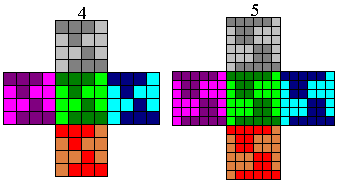
Deze schitterende plaatjes
kregen we van Roel Huisman. Zijn mieren niet alleen ijverig, maar hebben ze ook
nog inzicht?
Op
Nobnet vonden we een vraag van Karl
Scherer: verdeel de X-pentomino in n congruente
delen. In de volgende alinea’s geven we voor elke mogelijke n een aantal
voorbeelden. Als je nog andere verdelingen vindt en we mogen ze op onze site
gebruiken, mail dan naar
o.d.m@pi.be.
In 2 congruente
delen
vonden we oneindig veel mogelijkheden.
Elke rechte door het middelpunt verdeelt de X-pentomino altijd in twee
congruente delen.

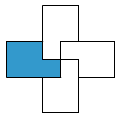
Iemand mailde ons dat er nog een andere mogelijkheid is om oneindig veel
mogelijke verdelingen in 2 congruente delen te maken en stuurde ons onderstaande
tekening:
In 4 congruente delen vonden we ook oneindig veel oplossingen.
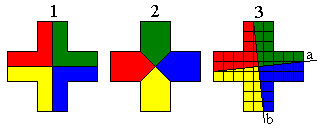
1) verdeling in vier congruente V-pentomino’s.
2) verdeling in vier “huisjes”
3) de rechten a en b staan loodrecht op elkaar(denk aan richtingscoëfficiënten).; elke draaiing levert een correcte oplossing, eigenlijk zijn oplossing 1 en 2 bijzondere voorbeelden hiervan.
De verdeling 3 kan op analoge manier verder door de zijde van de X-pentomino te verdelen in 4,5… gelijke delen.
Roel Huisman bezorgde ons nog en andere verdeling namelijk in 4 congruente P-pentomino’s.
Aad van de Wetering vond nog een andere mooie verdeling met 4 congruente Z-pentomino’s.(oplossing 1) . Op een gelijkaardige manier zijn er oneindig veel andere verdelingen in 4 congruente delen te vinden (zie bijvoorbeeld de oplossingen 2 en 3).
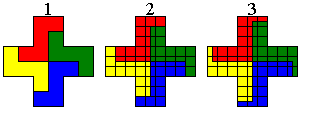

In 8 congruente delen vonden we eerst oplossing 1 en dankzij Aads verdeling in 4 congruente Z-pentomino’s vonden we oplossing 2:
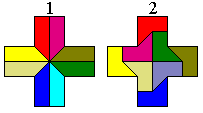
Aad mailde ons echter dat er voor de verdeling in 8 congruente delen oneindig veel manieren zijn en voegde er de oplossing 1 bij met de melding: je kan de lijntjes trekken zoals je maar wilt (wél door het snijpunt van de diagonalen van het vierkant), het komt altijd goed:
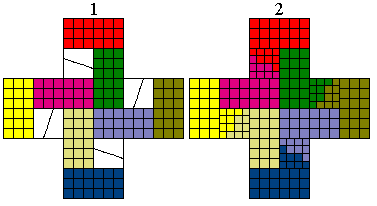
Dank zij de raad die we voor een verdeling in 10 congruente delen gekregen hebben, dachten we eraan dat het ook kon met een verdeling in trapjes (zie oplossing 2) en het kan dus ook met willekeurige krommen.
In 10 congruente delen vonden we eerst 2 mogelijkheden:
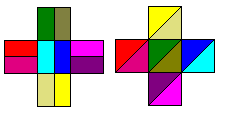
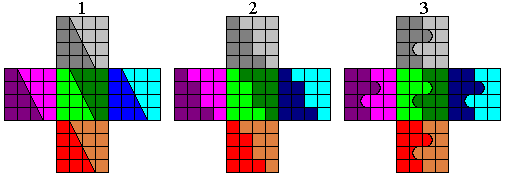
Iemand mailde ons echter: voor 10 zijn er ook oneindig veel, kijk maar:
1) als de rechte maar door het "middelpunt" van het vierkant gaat.
2) je kan ook nog trappetjes maken.
3) het kan ook met krommen.
De fantasie van onze mailster kent geen grenzen. Bedankt voor de oplossingen.
In 12 congruente delen kregen we twee oplossingen:
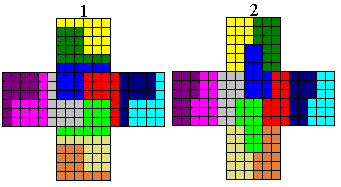
De eerste van Roel Huisman, de tweede van Aad van de Wetering.
Zouden Nederlanders dan toch slimmer zijn?
In 15 congruente delen vonden we zelf de gemakkelijke oplossing 1.
De mooie oplossing 2 waarbij de X-pentomino verdeeld wordt in 15 V-tromino’s kregen we van Aad van de Wetering.Voor het opvullen met de 15 V-tromino’s gebruikte Aad natuurlijk zijn eigen ‘Flatpoly’.
Het programma is vrij te downloaden op zijn site.
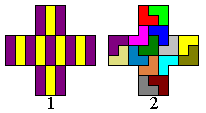
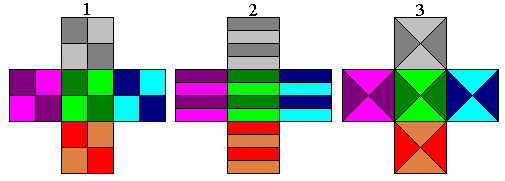
In 16 congruente delen:
We vergroten de zijde 4x en dan weten we dat de oppervlakte 16x groter wordt.We kunnen de X-pentomino dan vullen met 16 L – of met 16 P-pentomino’s.
Bijzonder fraai vinden we de
verdeling waarbij de X-pentomino eerst
verdeeld is in 4 congruente P-pento’s en daarna in 16.
Voor het opvullen met 16 pentomino’s gebruikten we Flatpoly van Aad van de Wetering.
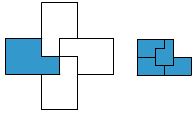
In 20 congruente delen:
Weer vonden we oneindig veel oplossingen. Eigenlijk zochten we naar
verschillende mogelijkheden om een vierkant te verdelen in 4 congruente delen.
Oplossing 4 vonden we vanuit de gekregen oplossing 2 bij een verdeling in 10 congruente delen.Dit is een verdeling die aanleiding geeft tot oneindig veel verdelingen in 20 congruente delen; zie bijvoorbeeld oplossing 5.
Om dit nog
duidelijker te maken hebben we 1 vierkant nog verder verdeeld in 4 congruente
delen:
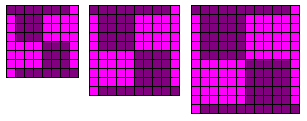
We vonden in het Doe-boek 9 “De veelzijdigheid van vierkanten” van Vierkant voor Wiskunde vraag 3.8 die we hier eigenlijk opgelost hebben.
De vraag: verdeel een vierkant van 6 bij 6 in 8 stukken: 4 L-tetromino’s en 4 Z-pentomino’s.
Vierkant 1 is de oplossing

We konden het niet laten van de vorm ook te zien als bestaande voor een deel uit de I-pentomino(vierkant 2) enerzijds of de V-pentomino(vierkant 3) anderzijds.
Aad van de Wetering kon het niet laten van ons een eenvoudiger manier door te mailen waarbij we ook oneindig veel mogelijke oplossingen krijgen namelijk door eenvoudig de lijnen te draaien van oplossing 3:

Een draaiing behoudt inderdaad de hoekgrootte.
Roel Huisman mailde ons
een prachtig overzicht van monomino tot hexomino waarbij hij telkens de
X-pentomino vulde met zo weinig mogelijk stukken. Roel
maakte eerst een vierkant met tetromino’s om nadien de X-pentomino op te vullen
met 20 congruente tetromino’s:
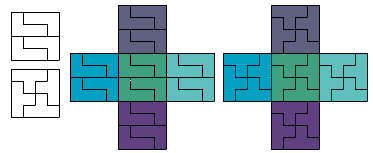
Opmerking: we kunnen de X-pentomino altijd verdelen in elk strikt positief 5-voud congruente delen.
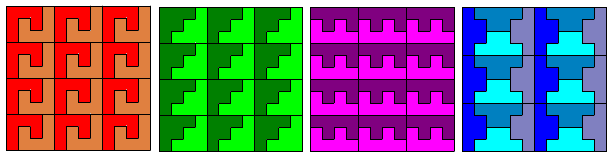
Marc Vuylsteke een ex-collega wiskunde van het TID Ronse kon het niet laten van een extra aantal verdelingen te tekenen in een aantal congruente pentomino’s .
.gif)

.gif)
.gif)
Deze verdelingen zijn inderdaad mooi omdat de X-pentomino eerst verdeeld is in 4 congruente P-pentomino’s (zie 1,2 en3) en nadien in 100 I- ,P- en L-pentomino’s.
Bij oplossing 4 en 5 is eerst verdeeld in 4 congruent Z-pentomino’s en nadien in 100 L- of 100 P-pentomino’s (Het kan natuurlijk ook met I-pentomino).
En Marc weet van geen ophouden (hij is trouwens met pensioen) of wil hij iets bewijzen aan de Nederlanders?
.gif)
Hier wordt de X-pentomino eerst verdeeld in 2 congruente delen, elk deel nadien in 5 (de X-pentomino dus in 10) en nadien wordt elke rechthoek gevuld met 10 pentomino’s (de X-pentomino) wordt dus verdeeld in 100 congruente delen.
Oplossing 3 vinden we vooral mooi omdat hierbij een rechthoek van 10x5 gevuld wordt met 10 Y-pentomino’s.
In 120 congruente delen:
Met 4 verschillende hexomino’s kon Roel een vierkant maken die 24 congruente
hexomino’s bevatte. De X-pentomino wordt dus verdeeld in 24x5=120 congruente
hexomino’s.
In 1080 congruente hexomino’s:
Roel maakte de volgende rechthoek mat 18 congruente hexomino’s.
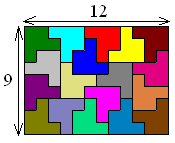
Met 12 van deze rechthoeken kunnen we een vierkant maken dat dus verdeeld is in
18x12=216 congruente hexomino’s.
De X-pentomino wordt dus verdeeld in 216x5=1080 congruente delen.
Opmerking:
we kunnen de X-pentomino altijd verdelen in elk strikt positief 5-voud
congruente delen.
Als je nog
andere verdelingen vindt en we mogen ze op onze site gebruiken, mail dan naar: