Vergroten en verdelen in congruente delen

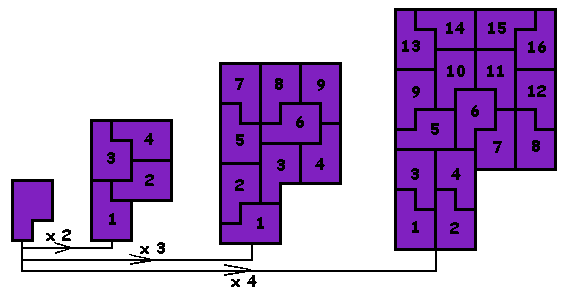
Als men een figuur afbeeldt door een gelijkvormigheid met factor 2 dan is de oppervlakte 4 maal groter geworden.
Vergroot men de lengtematen met 3 dan is de oppervlakte 9x groter.
Is de gelijkvormigheidsfactor 4 dan kan is de oppervlakte 16 maal groter .

We vergroten elke pento met factor 2.
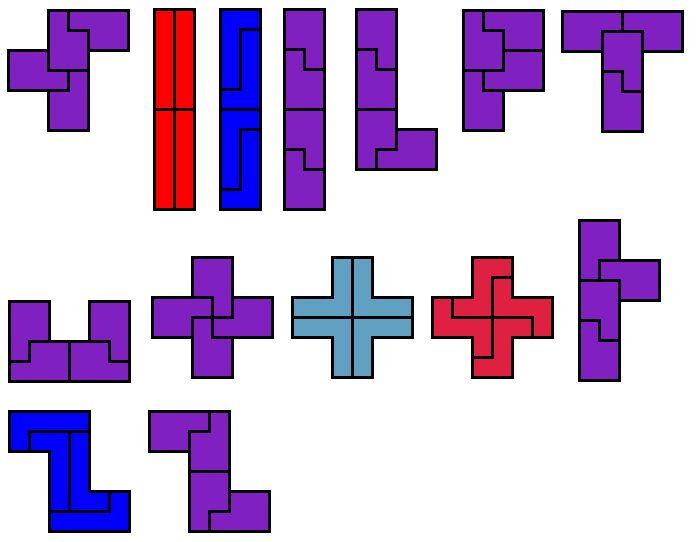
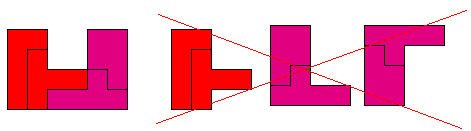
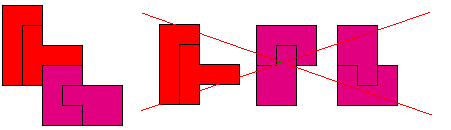
Sommige kunnen opgevuld worden met 4 congruente pentomino's.

We vergroten elke pento met factor 3.
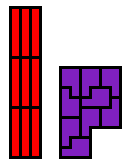
Alleen I- en P-pento kunnen opgevuld worden met 9 congruente pentomino's, toevallig ook nog alleen met 9 exemplaren van zichzelf.

We vergroten elke pento met factor 4.
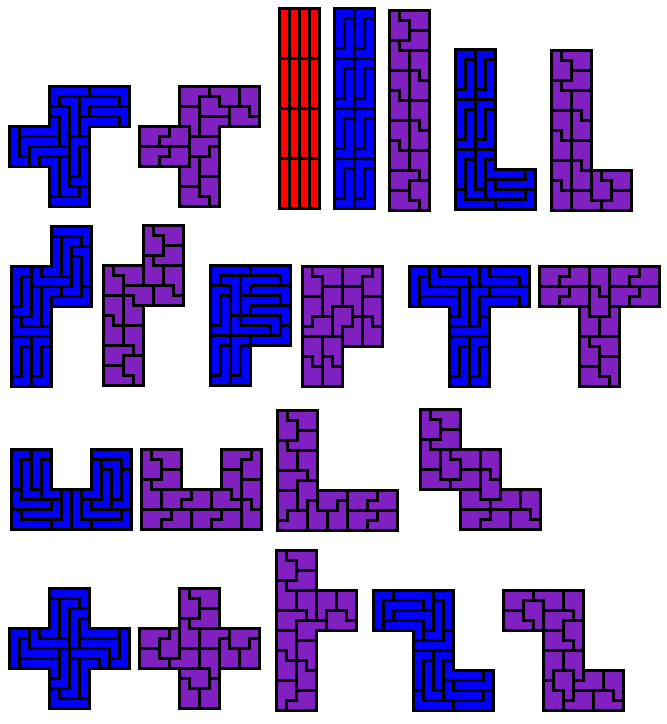
Sommige kunnen opgevuld worden met 16 congruente pentomino's.

We vergroten opnieuw elke pentomino met factor 2.
We proberen hem te vullen met 2x2 identieke pento's.
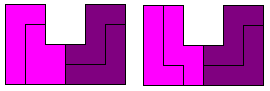
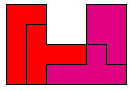
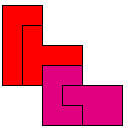
We vonden enkele voorbeelden waarbij de pento ook nog verdeeld is in 2 congruente delen.

Meestal vergroot men pentomino's en probeert men ze te vullen met een aantal uit één set.
Bij de U en Z-pento vonden we een verdeling in 2 congruente delen

Soms is het even zoeken of delen congruent zijn.

Figuren met dezelfde oppervlakte zijn niet noodzakelijk congruent.

Commentaar is altijd welkom.
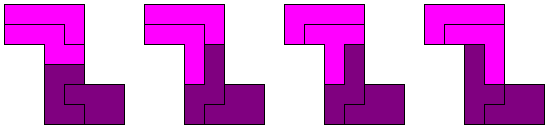
o.d.m@pi.be