Congruentie en gelijkvormigheid
 

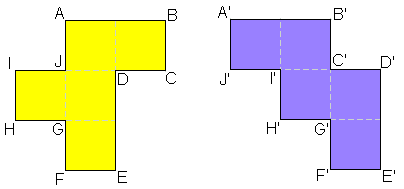
We vroegen ons om te beginnen iets anders af:"Bestaan er twee veelhoeken, waarvan de lengten van de zijden twee aan twee gelijk zijn en waarvan de hoeken paarsgewijs even groot zijn en die toch niet congruent zijn?"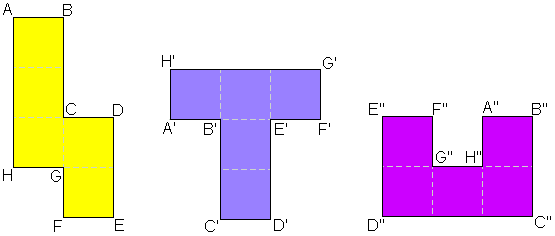

Achthoeken

 Maatgetal van de zijden:
 Er zijn telkens vijf zijden met maatgetal 1, twee zijden met maatgetal 2 en één zijde met maatgetal 3

Grootte van de hoeken
Er zijn telkens zes hoeken van 90° en twee hoeken van 270°

De pentomino's zijn echter niet congruent!
De oorzaak is dat het niet altijd overeenkomstige hoeken (hoeken ingesloten door twee aan twee gelijke zijden) zijn die gelijk zijn.

 Tienhoeken

Maatgetal van de zijden:
 Er zijn telkens acht zijden met maatgetal 1 en twee zijden met maatgetal 2.

Grootte van de hoeken
Er zijn telkens zeven hoeken van 90° en drie hoeken van 270°

De pentomino's zijn echter niet congruent!
Verklaring: zie hierboven

En nu het antwoord op de vraag:"Bestaan er twee veelhoeken, waarvan de lengten van de zijden recht evenredig zijn en waarvan de hoeken paarsgewijs even groot zijn en die toch niet gelijkvormig zijn?"

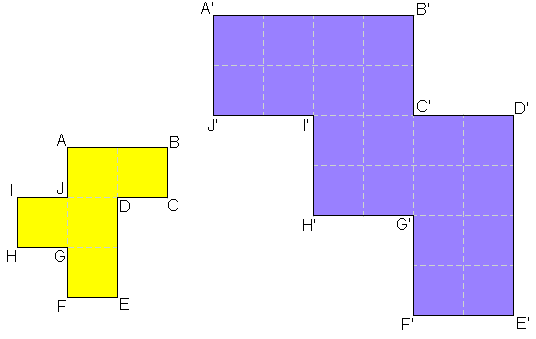
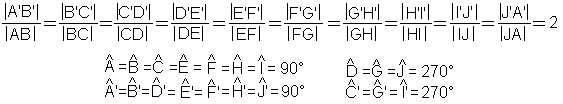
De pentomino's zijn niet gelijkvormig.
Dit komt doordat het niet altijd de overeenkomstige hoeken zijn (hoeken ingesloten door evenredige zijden) die gelijk zijn.
Voorbeeld: hoek C is verschillend van de hoek C'