We kregen een mail van Aidan Burns:
"I used to have a little book by Sivy Farhi which had many pentomino puzzles.
There's the problem of making a shape which contains a copy of itself within it. An example of this is a 10x6 rectangle with a 5x3 sub-rectangle, but there are many others.
And a lovely problem is to use 9 sets of pentominoes to make triple sized copies of all the pentominoes, and within each copy you can't use the same pentomino twice."
We kenden de problemen.
Het laatste kan je mooi uitgewerkt vinden op de site van Aad van de Wetering.
We werkten de eerste opgave een beetje uit omdat we dit een mooie toepassing op gelijkvormigheid vinden.
De kopie (oppervlakte = S) en de gehele figuur (oppervlakte 12x5 = 60) zijn gelijkvormig.
Als de gelijkvormigheidsfactor van de figuur t.o.v. de kopie 2 is dan gaat de oppervlakte 4 maal groter zijn.
4S = 60 => S = 15

We zochten nog 16 andere voorbeelden.
Het kopie bestaat uit 3 pentomino's en dit geheel is gelijkvormig met de totale figuur. (12 pentomino's = 4x meer)
Het kopie ligt soms gedraaid of gespiegeld.
De cijfers die bij de vormen staan verwijzen naar de oplossingen die we van Helmut Postl kregen.(zie verder)
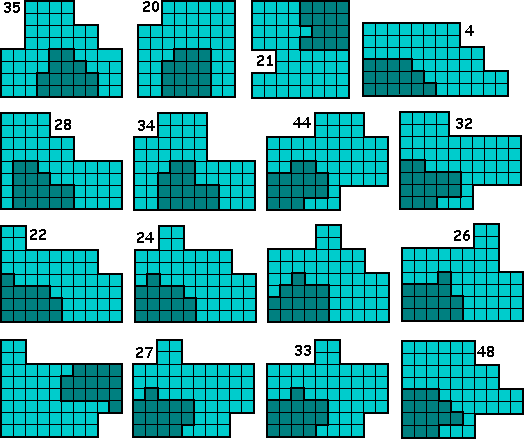
FlatPoly zocht opnieuw voor ons de oplossingen.
Wil je een oplossing zien klik dan op de bovenstaande tekening.
Vind je er nog andere?
We plaatsen ze heel graag bij op deze pagina.
We waren heel blij dat er reeds iemand onmiddellijk inzond.
De tweede vorm staat reeds op de site.

Ook Peter Jeuken zond ons een oplossing.

We kregen oplossingen van Helmut Postl (Wenen)
"These patterns are all that I have found, but I am not sure that they are all. I looked only for patterns where the small pattern has the same orientation as the big pattern (no rotation, no turnover)."
Hij mailde ons een tekstbestand met 18 pagina's oplossingen.
We begonnen met veel moed en vulden zijn vormen aan met oplossingen waarbij de kleine vorm wel gedraaid of gespiegeld is.
We zijn bewust van de onvolledigheid van de oplossingen.
Toch denken we dat Helmut vrij volledig is. Er zijn dus 88 (verschillende) vormen als de gelijkvormige figuur dezelfde oriŽntatie heeft.
Er staat telkens een overzicht van de kleine vormen bovenaan.
Voor de oplossingen druk op de opgave.
Rechthoek 3x6




Rechthoek 3x7

Rechthoek 4x4 en 4x5

Van vorm 20 denken we dat we alle oplossingen(22) hebben.
Hij is ook wel speciaal omdat hij een schuine symmetrie-as heeft. In de eerste oplossing heeft ook het geheel zonder de kleine vorm een symmetrie-as. We denken dat dit enig is.











Rechthoek 4x6



Rechthoek 3x8



