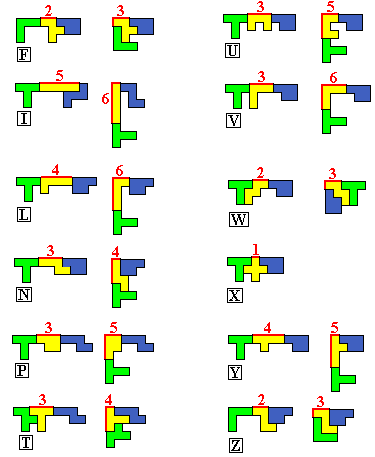
Bijdrage van verschillende pentomino’s voor het vormen van omtrek van ingesloten rechthoek

Pentomino

Niet in de hoek

In de hoek

Winst of verlies

Verlies totale omtrek

F

2

3

1

-

I

5

5

-

-1

L

4

4

-

-

N

3

3

-

-1

P

3

3

-

-1

T

3

3

-

-

U

3

3

-

-1

V

4

4

1

-

W

2

2

-

-

X

2

2

1

-

Y

4

4

-

-1

Z

3

3

1

-

Totaal

35

 

 

 
Om over een maximale omtrek te beschikken gaan we F,V,X en Z kiezen in de hoeken.
We beschikken dan over 35+4=39 eenheden van de pentomino’s.
Voor de kleinste brug gebruiken we zo weinig mogelijk van de 39 eenheden.
We maken gebruik van X,W en Z(of F)
We gebruiken hiervoor 2+2+3=7 eenheden (Ingesloten oppervlakte 5)
We beschikken nog over 32 eenheden.Hiermee moet de ingesloten rechthoek een maximale oppervlakte bezitten.
Dit is als de lengte 16 en de hoogte 8 is.(Oppervlakte=128)
De totale ingesloten oppervlakte van de 2 bruggen is dan 128+5=133

Naar de vorige pagina