Pento-KenKen

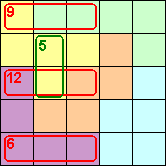
Als de som van 3 getallen 6 moet zijn dan zijn die getallen 1, 2 en 3=>5 moet op d1 of e1.
In de P-pentomino kan 5 dus niet op d2, e2 en e3.
Als de som van 3 getallen 12 moet zijn dan zijn die getallen 3, 4 en 5 => 5 kan niet op d3 (ook niet op e3 maar dat wisten we al).
Omdat de som van de getallen die op b3 en b4 staan 5 is kan 5 daar niet staan.
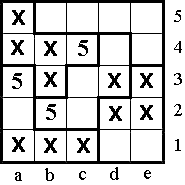
In V-pentomino moet 5 op a2 of a3=> 5 kan niet op a4 of a5 => 5 moet in de F-pento op c4 en in de W-pento op b2=>5 moet op a3 en dus moet 4 op a2.
In F-pento moet 4 dus op b3 of b4 dus is het andere getal 1 (som 5)=> in eerste kolom moet 1 op a1.
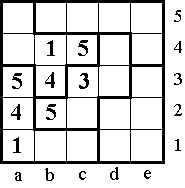
Als de som van 3 getallen 9 moet zijn dan zijn die getallen 1, 3 en 5 of 2, 3 en 4. Aangezien 5 niet op a5,b5 of c5 kan moet die combinatie wel 2,3 en 4 zijn =>4 moet op c5 (want kan niet op a5 en b5)
In b3 moet 4 staan want b3 en b4 zijn 1 en 4 en a3,b3 en c3 zijn 3,4 en 5.
Eerst vullen we de V-pento aan en dan de kolommen.
Dan verder via de W-pento naar het eindresultaat