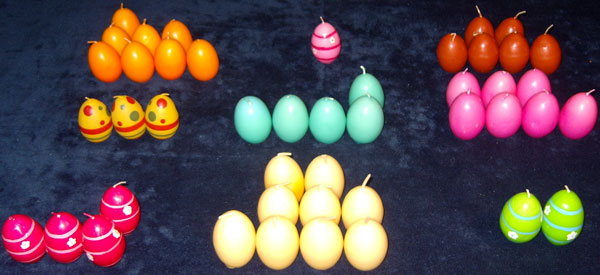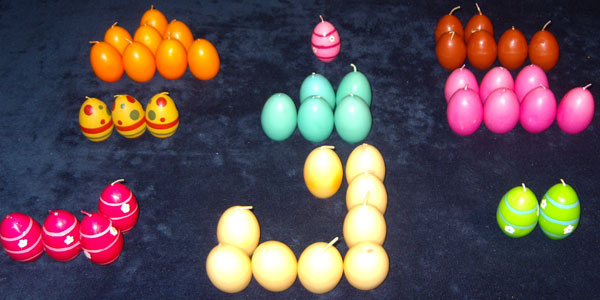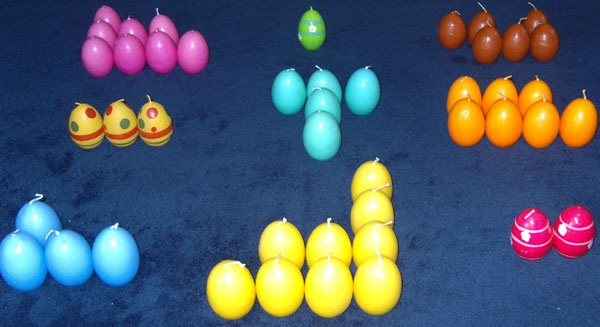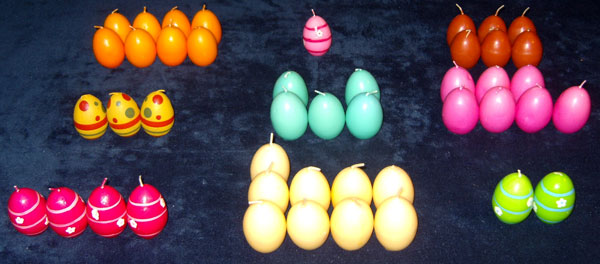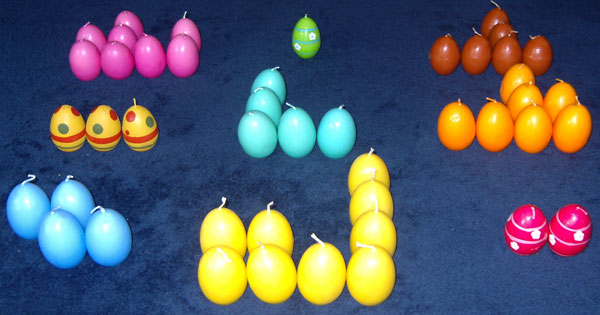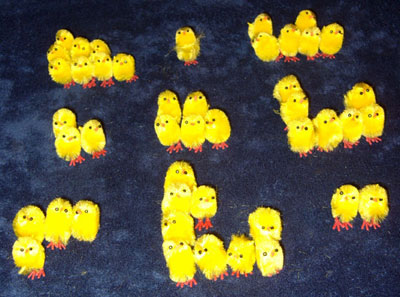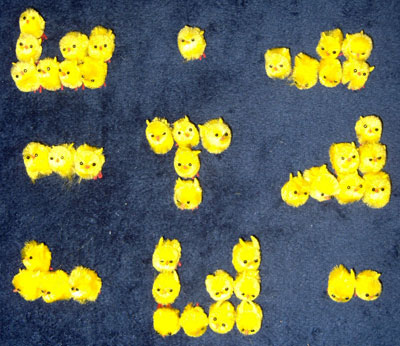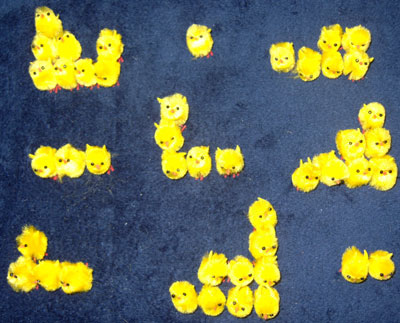Pento-magisch vierkant

In een magisch vierkant is de som van de getallen in alle rijen, kolommen en diagonalen hetzelfde.
We vertrekken van het volgende magische vierkant

Lee Sallows had het lumineus idee van de getallen te vervangen door figuren . Met deze figuren van elke rij, van iedere kolom en van de diagonalen moet steeds dezelfde vorm worden gelegd.
Matthijs Coster maakte hierover de prijsvraag voor het tijdschrift Pythagoras.
Neem in plaats van de getallen even zoveel aaneengesloten vierkantjes. Zo ontstaan negen figuren. Doe het zo, dat je een geomagisch vierkant krijgt waarvan het doel een vierkant is
Aangezien er voor vraag 4 al 205 oplossingen zijn die we allemaal getekend hebben
http://users.fulladsl.be/~spb33365/Vraag4goed1.ppt
http://users.fulladsl.be/~spb33365/Vraag4goed2.pps
willen we voor vraag 5 een beperking stellen., namelijk met een verschillende pentomino in het midden.
Voor onze wedstrijd 47 kregen we er al een aantal binnen.
Bij het eerste doel is een hoekvierkantje weggelaten

De bedoeling is om zelf op te lossen.
Wil je echter de oplossing zien druk dan op de foto.

L-pentomino


N-pentomino


P-pentomino


T-pentomino

U-pentomino


V-pentomino


W-pentomino


Y-pentomino


Dank aan Helmut Postl voor de oplossing met de F-pentomino


Dat X en Z-pentomino geen oplossingen hebben legde Helmut heel mooi uit in een pdf-bestand

Bij het tweede doel is er een vierkantje van de rand weg maar niet in de hoek
Dank aan Bob Henderson voor de oplossing van T,V en W-pentomino


L-pentomino


P-pentomino


T-pentomino


U-pentomino


V-pentomino


W-pentomino