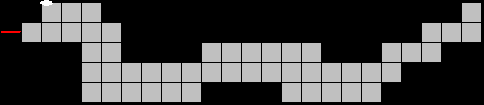
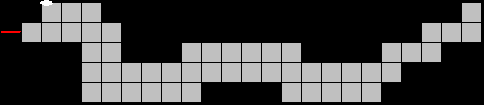
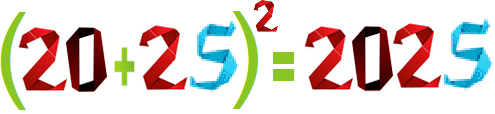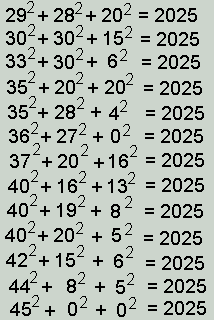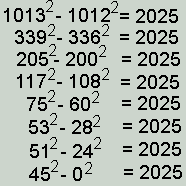"2025" is gevuld met een
hexominoset (35 verschillende vormen van 6 vierkantjes)
We beginnen onze pagina traditiegetrouw met het supermooie nieuwjaarsgedicht van Marjolein
Kool. Dank

Een bijzondere eigenschap
is:
(1+2+3+4+5+6+7+8+9)² = 2025
De vorige keer dat een jaartal een kwadraat was, was 89 jaar geleden: 1936 =
44².
Na 2025 moeten we 91 jaar wachten totdat zich weer een kwadraatjaar
aandient: 2116 = 46².
Helmut Postl wees op een heel mooie gelijkheid
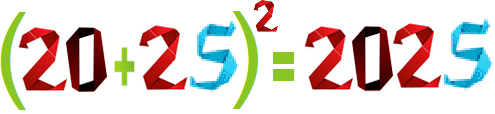
Wat ook heel mooi is:
1³+2³+3³+4³+5³+6³+7³+8³+9³ = 2025
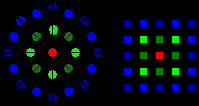
2025 is een gecentreerd achthoekig getal:
2025 = 1+1x8+2x8+3x8+4x8+5x8+6x8+7x8+8x8+...+20x8+21x8+22x8
We maakten hiervan een voorstelling en wensen dat 2025 even kleurrijk mag
zijn.
De gecentreerde achthoekige getallen zijn hetzelfde als de oneven
kwadraatgetallen.
|
 |
 |
Helmut herhaalde wat we proberen
voorstellen hadden met de bovenstaande tekeningen:
"Nice idea! I realized that you can transform every odd square into an
octagon. Just draw the four axes of symmetry into the given square. They
divide the square into eight octants. Now shear each octant a bit such that
the sides have the right slope for an octagon."
We stelden de eerste 2 achthoeken opnieuw voor met wat ruimte tussen.
We wensen iedereen een jaar vol magie.
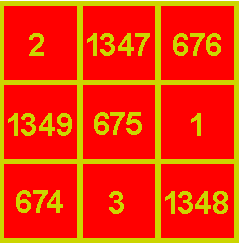
Vierkant met magische constante 2025.
Volgens Matthijs en Helmut zijn er 113008 verschillende.
Het jaartal moet een drievoud zijn om een magisch vierkant te kunnen maken
van 3x3.
Ook Ilse Deboeck stuurde een
magisch vierkant.

Traditiegetrouw kregen we van Paul Levrie en Rudi Penne een
nieuwjaarskaartje.

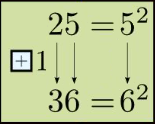
Helmut mailde : "Fine things on the site! Especially the New Year's
card by Paul and Rudi with 2025 = 45² ---> 3136 = 56².
There is only one more such number, that is 25 = 5² ---> 36 = 6². That's all
of them!
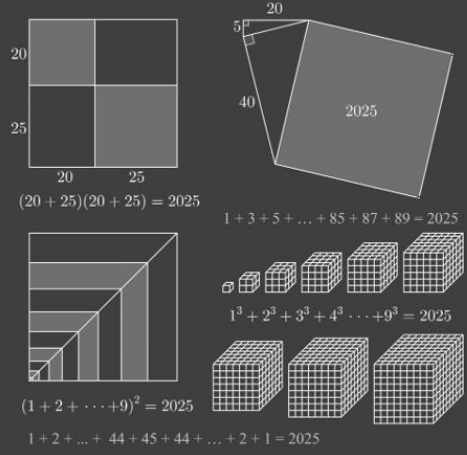
In Roer (door Luc Gheysens en Thomas Goorman) stond een heel mooi plaatje
met wetenswaardigheden over 2025.
Er stond ook een heel leuke rekenklok voor 2025.

De leerlingen
uit
het Sint-Angela
in Ternat kregen
een opdracht om
2025 met 0,1,2,3,4,5,6,7,8,9
in volgorde met +, -, x, :, plakken en faculteit te vinden.
We zochten er ook enkele:
(0x1+2+3)x(4+5)x(6+7-8)x9=2025
(0-1x(2-3)x4x56-7+8)x9 =2025
(0+1+2+3+4!+5!+67+8)x9 =2025
(0+123+4+5!:6+78)x9=2025
(0+1-23+(4!-5):6x78)x9=2025
(0+12x3:4)x5x(6+7-8)x9=2025
((0!+1+2)!-3+4!)x((5:6!:7:8x9!)=2025
((0!+1+2)!-3+4!)x(5!-6-78+9)=2025
(0+1+2x3x4)x((5+67):8x9)=2025
(0+1x(23+4))(5x(6-(7-8)x9)=2025
(0+1+2+3x4!)x(5!-6-78-9)=2025
0+12x3+4x5!+6!+789=2025
0+123+4x5!+6!+78x9=2025
(0+1+2)x(3x45x6-(7+8)x9)=2025
0+12x(34+56+78)+9=2025
0+(1+2)!-(34x(5-67)+89)=2025
0!+1!-2+(3-4!)x(5!-6!):7:8x9=2025
0+(1+2)!+(34+5!)x(6+7)+8+9=2025
0+(1+2)!+3!+4x(56+7)x8-9=2025
0+12+3x(4+5!x6-7x8)+9=2025
Wat je natuurlijk jaarlijks kan aanpassen is onze rekenrups.
De reeks begint met het jaartal en bestaat uitsluitend uit positieve
getallen. Het volgende getal is steeds het verschil van de twee voorgaande.
De opdracht: zorg dat de reeks zolang mogelijk is.
Fibonacci is de sleutel.

Op 29 januari 2025 begint het jaar van de slang.
We maakten hiervoor een phibono
https://phibono.jouwweb.be/door-het-jaar-heen-19
Vul beide slangen met 10 verschillende pentomino's.
Er is telkens juist één oplossing.
Stuur je oplossing naar
OdetteDM@outlook.com
Zeker niet vergeten : 24 juli
2025 is een pythagorasdatum omdat 24²+7²=25²
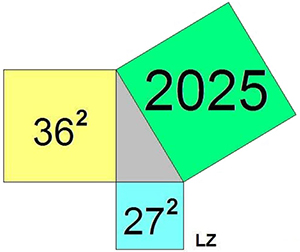
Livio Zucca zette deze tekening op facebook.
Luc Gheysens had nog een aanvulling:
"Er zijn 13 oplossingen om 2025 te schrijven als som van drie kwadraten"
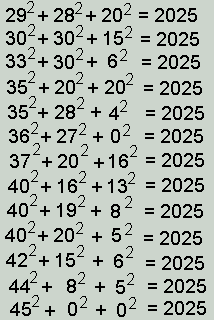
Luc De Wilde had ook een mooie
aanvulling:
"2025 kan geschreven worden als een verschil van kwadraten op acht
verschillende manieren."
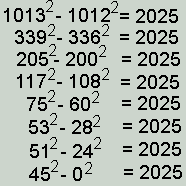
Hij stuurde een document met een mooie uitleg om deze te vinden (toepassing
op merwaardige producten en oplossing vqn stelsels)
Martin Kindt: "Ja, 2025 is een wiskundig rijk getal.We moeten er 1000
jaar op wachten voor we weer een kwadraat van een driehoeksgetal krijgen,
maar of er dan nog jaartelling op onze planeet gebeurt?"
Inderdaad, het volgend driehoeksgetal is 55 en 55²=3025