Leefruimte voor de pentomino's

Dit is puzzel 795 uit het vakblad Euclides.
De twaalf pentomino's worden op een vierkant eenheidsrooster geplaatst met de randen van de pentomino's langs de roosterlijnen.
De pentomino's raken elkaar niet, zelfs niet met een hoekpunt, en ze komen evenmin tegen de rand.
Probeer de rechthoek te vinden met de kleinst mogelijke oppervlakte. Hieronder is het voorbeeld uit Euclides.
De rechthoek heeft een oppervlakte van 12x17=214

We deden zelf enkele pogingen:

Leefruimte van 15x13=195

Leefruimte van 16x12=192

We kregen oorspronkelijk van Aad een leefruimte van 180.


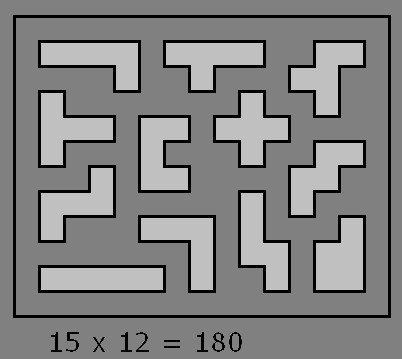
Deze oplossingen kunnen leuke variaties zijn op het gestelde probleem vooral als leerlingen het moeilijk vinden van naar de minimale oplossing te zoeken.

Nadat we van Helmut Postl uit Oostenrijk een oplossing van 176 gekregen hadden , vond Aad van de Wetering er ook één Van Tamme Afman kregen we zijn oplossing die hij voor Euclides gemaakt had.

Vind je nog andere leefruimtes?
Mail ze ons, we plaatsen ze graag op onze site.
o.d.m@fulladsl.be

F. Göbel maakte bij de puzzelopgave een bemerking waarmee we volledig akkoord zijn en die we hier dus graag publiceren.
 " Moet men puzzels die met een computer kunnen worden opgelost vermijden?
Sommige opgaven worden inderdaad erg eenvoudig als men er een programma voor schrijft. Aan de andere kant: wie besluit om een opgave door de computer te laten oplossen , mist het genoegen van het zelf puzzelen. Bovendien moet je er dan nog steeds zelf iets voor doen, namelijk een programma schrijven. Als een computer van nut kan zijn bij het oplossen van een opgave, dan nog kan ieder er op zijn eigen wijze genoegen aan beleven. "