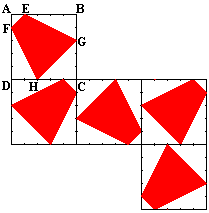
We vonden de inspiratie voor deze vraag bij de Vlaamse Wiskunde Olympiade 1997-Tweede ronde.
In elk vierkant met zijde 5
cm van de Z-pentomino is een gelijkbenig trapezium ingeschreven.
Bepaal de oppervlakte van het trapezium.

De oppervlakte van het trapezium is gelijk aan het verschil van de oppervlakte van een monomino en de oppervlaktes van de vier rechthoekige driehoeken
Oppervlakte driehoek AFE = (1 x
1) : 2 = 0,5
Oppervlakte driehoek FDH = (4 x 2) : 2 = 4
Oppervlakte driehoek HCG = (3 x 3) : 2 = 4,5
Oppervlakte driehoek GBH = (2 x 4) : 2 = 4
Oppervlakte trapezium = 25 cm² - 13 cm² = 12 cm²
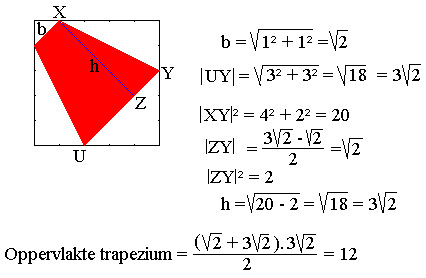
We hadden deze oefening ook
kunnen oplossen door de formule oppervlakte trapezium = (B + b) . h : 2 en de
afmetingen te bepalen met de stelling van Pythagoras.
Merk op dat de rode oppervlakte
48 % is van de Z-pentomino.