We vonden de inspiratie voor deze vraag bij de Vlaamse Wiskunde Olympiade 2004-Eerste ronde.
Bepaal de zijde van het kleinste vierkant dat zonder overlapping kan worden overdekt met papiersnippers die de vorm hebben van de L-pentomino, waarbij elk ruitje een vierkantje met zijde 1 is.
![]()
Aangezien de oppervlakte van een
pentomino 5 is moet de oppervlakte van het gevraagde vierkant een veelvoud van
5 zijn.
Het is niet mogelijk om een vierkant met zijde 5 te overdekken met
L-pentomino's, zonder overlapping.
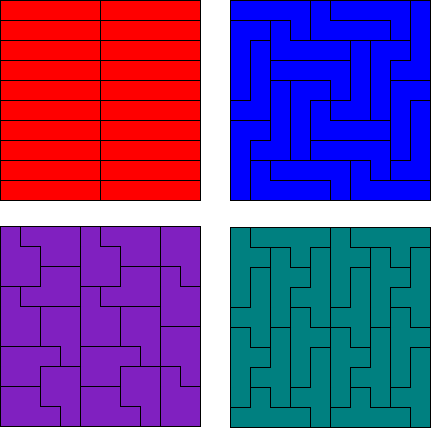
Dit lukt wel voor een vierkant met zijde 10.

We breiden dit probleem uit en vragen ons af met welke pentomino we een
vierkant met zijde 5 kunnen bedekken.
Dit kan alleen met de I.

Voor een 10 x 10 vierkant hebben we 4 mogelijkheden: