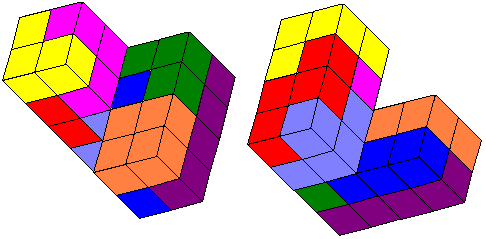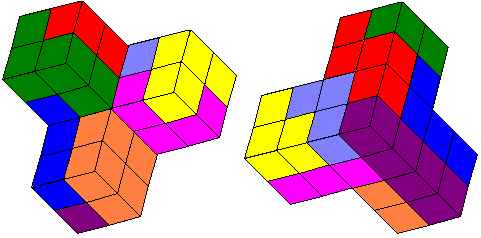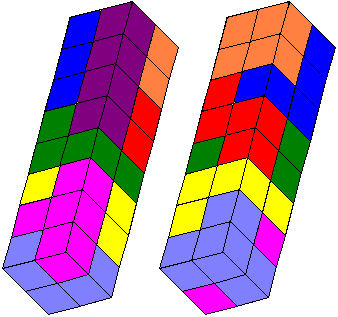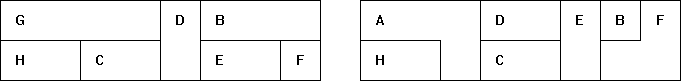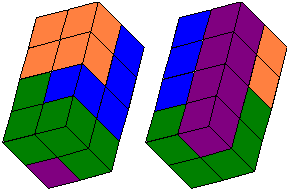Vraag 26

We kregen de kans samen met Leo Prinsen een artikel te schrijven voor "Volgens Bartjens".
Leo vond de titel "Mino-meetkunde" en ook de opgave voor een prijsvraag over een driedimensionaal gelijkvormigheidsprobleem.
Het probleem:
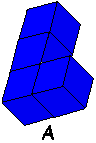
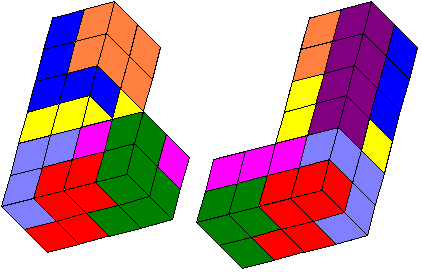
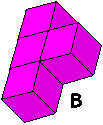
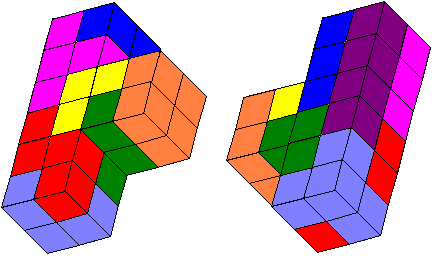
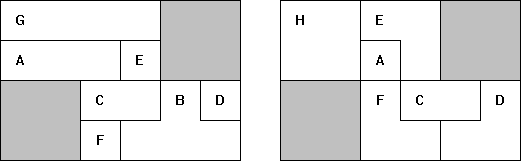
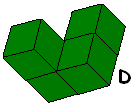
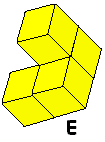
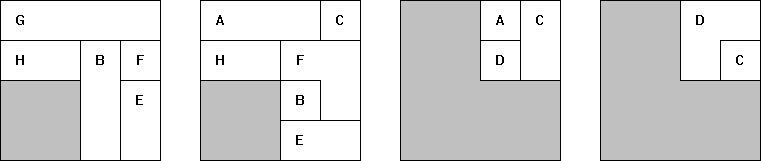
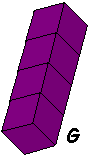
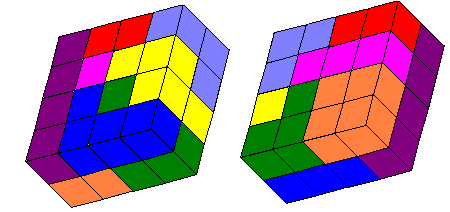
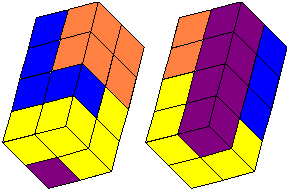
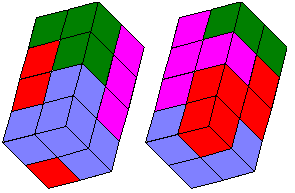
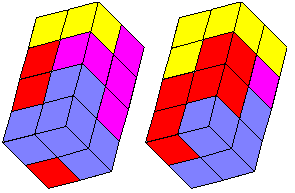
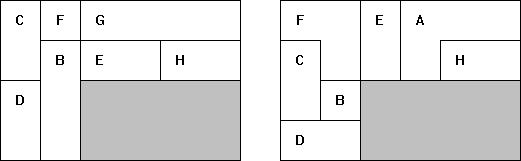
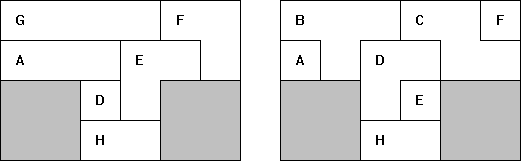
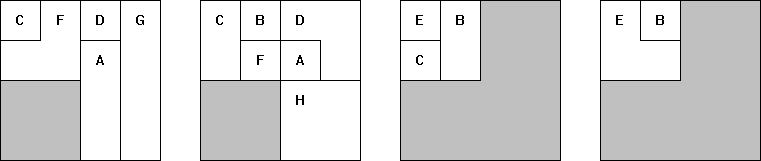
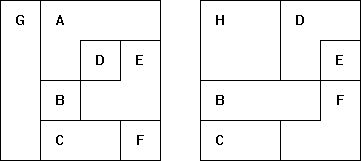
De serie tetrokubo’s bevat 8 exemplaren. Bouw een exemplaar in het groot na met gebruikmaking van de complete serie. Maak bovendien een bouwplan met behulp waarvan een ander jouw bouwsel kan namaken.
En tot slot: doe dat alles voor zoveel mogelijk en misschien wel alle exemplaren.

Omdat niemand hiervoor onmiddellijk tijd heeft gevonden en we dit een heel mooi probleem vinden vroegen we hulp aan Aad van de Wetering en gingen we zelf aan de slag.
Op de pagina van Aad kan je het programma Poly (191 kB gezipt) voor het vullen van een willekeurige driedimensionale ruimte met polyomino's downloaden.

 

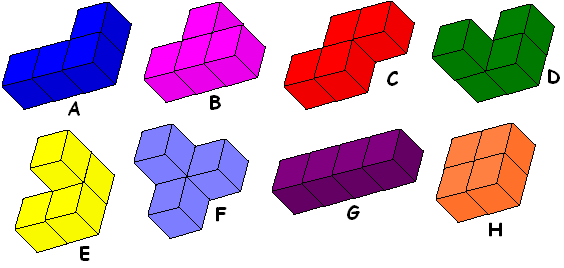
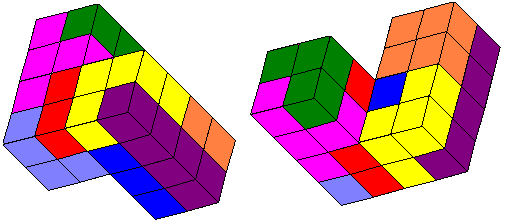
Wat dit probleem zo mooi maakt is dat men heel goed ziet dat als de gelijkvormigheidsfactor 2 is de inhoud 2³=8 maal groter wordt.
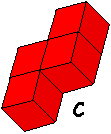
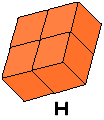
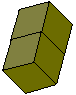
We hadden nog eenvoudiger kunnen beginnen namelijk met het zoeken naar de verdubbeling van een dokubus.
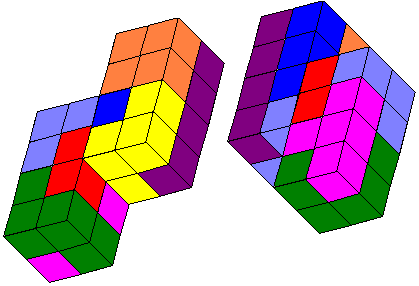
Dit is niet zo moeilijk maar je moet natuurlijk een tweede vergroting kunnen maken met de vier overblijvende tetrokubussen.
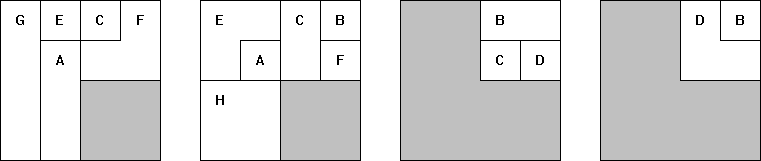
Hiermee kunnen we dan de vergroting van A-C-D-E-G-H maken.

Ook hier merken we op dat voor de vergroting (gelijkvormigheidsfactor 2) er 2³=8 maal meer kubussen nog zijn.
Heb je opmerkingen, andere oplossingen of heb je er in de klas iets mee gedaan dan willen we dat heel graag horen!