We kregen een mail van Aidan Burns:
"I used to have a little book by Sivy Farhi which had many pentomino puzzles.
There's the problem of making a shape which has a hole similar to the whole shape. Examples of this are the 8x8 square with a 4x4 hole and the 10x8 rectangle with a 5x4 hole, but there are many others."
We kenden het probleem maar het stond nog niet op de site dus werkten we eraan.
Het gat (oppervlakte = S) en de gehele figuur zijn gelijkvormig.
Als de gelijkvormigheidsfactor van de figuur t.o.v. het gat 2 is dan gaat de oppervlakte 4 maal groter zijn.
4S-S = 3S = 60 => S = 20

We zochten nog 9 andere voorbeelden.
Het gat is steeds gelijkvormig met de totale figuur. Met de plaats van het gat wordt geen rekening gehouden.
Het gat mag ook gedraaid of gespiegeld worden.

FlatPoly zocht opnieuw voor ons de oplossingen.
Wil je een oplossing zien klik dan op de bovenstaande tekening.
We willen er één afzonderlijk vermelden omwille van de verticale symmetrie-as die de figuur (zonder gat) bezit!

Vind je er nog andere?
We plaatsen ze heel graag bij op deze pagina.
De eerste die er ons 3 toestuurde was Aad van de Wetering en zelfs alle drie met een verticale symmetrie-as.
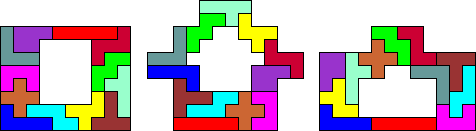
Knap gevonden!
En dan kregen we een inzending van Helmut Postl (Wenen). Zijn tekstbestand telt maar liefst 55 pagina's.
Volledig is het niet in die zin dat hij mailde: "I looked only for patterns where the small pattern has the same orientation as the big pattern."
Hieronder staan de verschillende gaten. Het zijn er 297 (als we juist gewerkt hebben ?)
Sommige kunnen op verschillende plaatsen binnen de vorm voorkomen.
In een rechthoek van 4x6

In een rechthoek van 3x8
In een rechthoek van 4x5

In een rechthoek van 5x5
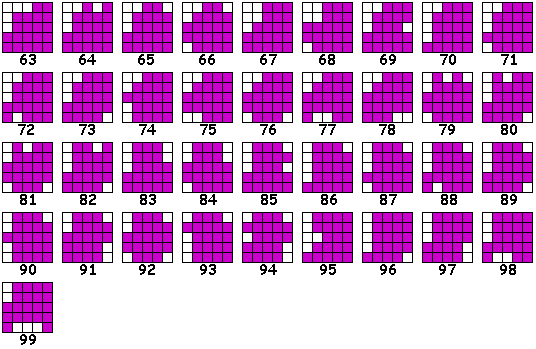
In een rechthoek van 4x7

In een rechthoek van 6x5

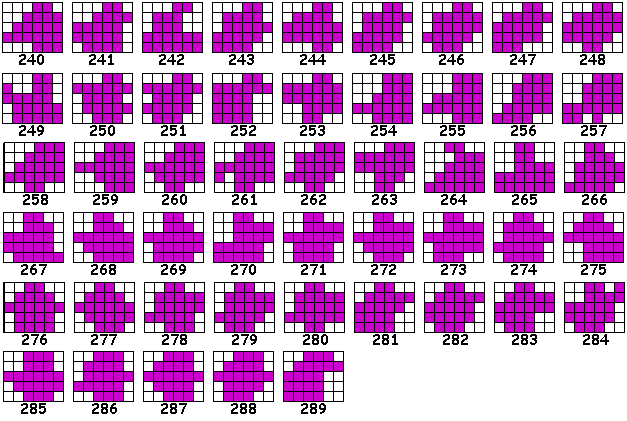
In een rechthoek van 4x8
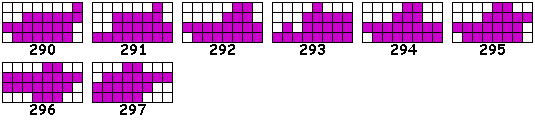
Als de gelijkvormigheidsfactor van de figuur t.o.v. het gat 3 is dan gaat de oppervlakte 9 maal groter zijn.
9S-S = 8S = 60 => S = 7,5
Dit lukt niet met onze pentomino's.
Als de gelijkvormigheidsfactor van de figuur t.o.v. het gat 4 is dan gaat de oppervlakte 16 maal groter zijn.
16S-S = 15S = 60 => S = 4
Hiervan is het vierkant van 8x8 met in het midden een vierkant een bekend voorbeeld.
Aangezien het gat een oppervlakte van 4 heeft zijn de verschillende vormen de tetromino's.
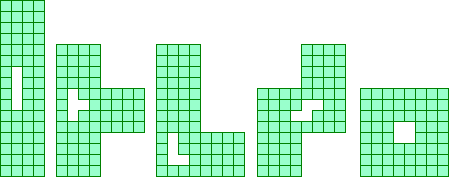
Wil je een oplossing zien klik dan op de bovenstaande tekening.
Het probleem van een vierkant min een vierkant te vullen met pentomino's deed denken aan een mooie opdracht uit het boekje van enkele leraars van het CSG Liudger te Drachten-Friesland-Nederland over pentomino’s.
Ze waren geïnspireerd door onze presentatie op de Nationale Wiskunde Dagen te Noordwijkerhout.
Je kan het boekje hier downloaden.
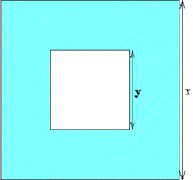
Het is mogelijk om de gekleurde rand met pentomino’s op te vullen.
Hiervoor moet gelden dat x²-y²=60
Het zoeken van alle natuurlijke oplossingen van de vergelijking: x²-y²=60 is een mooie toepassing op het ontbinden in factoren en het oplossen van stelsels met 2 vergelijkingen en 2 onbekenden.