Betegelingen
In Euclides (= Vakblad voor de wiskundeleraar) van de
Nederlands Vereniging van Wiskundeleraren stond in het blad van
april 2008 bij recreatie deze pentomino-puzzel. De meeste vreugde heb je als
je hem eigenhandig vindt, maar wij maakten gebruik van het schitterend
programma van Aad van de Wetering
FlatPoly die het probleem ongelooflijk snel
oplost.
Opgave 1
Betegel voor ieder van de pentomino's een rechthoek met één of meer
kopieën van de pentomino en van een domino.
Streef hierbij steeds naar een rechthoek met een zo klein mogelijke
oppervlakte.

Dat zijn dus in feite 12 opgaven waarvan de meeste triviaal zijn.
De som van de oppervlakten in ons oplossing is 164.
Kan je het beter?
Goede oplossers verwerven eeuwige roem.
Mail naar:
o.d.m@fulladsl.be
| Naam |
Land |
Opgave
1 |
| Frits Göbel |
Nederland |
158 |
| Aad van de Wetering |
Nederland |
163 |
| Helmut Postl |
Oostenrijk |
158 |
| Peter Jeuken |
Nederland |
158 |
| Lieke de Rooij |
Nederland |
158 |
| Nico Looije |
Nederland |
158 |
Opgave 2
Bepaal een rechthoek die kan worden betegeld met de I-tromino en de
Z-pentomino.

We vonden een oplossing met oppervlakte 42.
Kan je het beter?
Goede oplossers verwerven eeuwige roem.
Mail naar:
o.d.m@fulladsl.be
| Naam |
Land |
Opgave
2 |
| Aad van de Wetering |
Nederland |
42 |
| Helmut Postl |
Oostenrijk |
42 |
| Martin Friedeman |
Nederland |
42 |
| Peter Jeuken |
Nederland |
42 |
| Lieke de Rooij |
Nederland |
42 |
|
Nico Looije |
Nederland |
42 |
George Sicherman: "Here is a
square solution"

Opgave 3
Bepaal een rechthoek die kan worden betegeld met de O-tetromino en de
T-pentomino.

We vonden een oplossing met oppervlakte 80.
Kan je het beter?
Goede oplossers verwerven eeuwige roem.
Mail naar:
o.d.m@fulladsl.be
| Naam |
Land |
Opgave
3 |
| Aad van de Wetering |
Nederland |
80 |
| Helmut Postl |
Oostenrijk |
80 |
| Martin Friedeman |
Nederland |
80 |
| Peter Jeuken |
Nederland |
80 |
| Lieke de Rooij |
Nederland |
80 |
| George Sicherman |
USA |
80 |
tr>
Nico Looije |
Nederland |
80 |
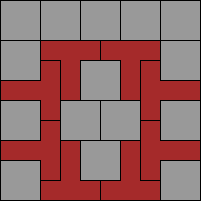
George Sicherman:"Here is a
complementary square for the T pentomino. (For 4-rotary symmetry, you will
need a 14x14 square.)"
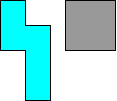
George Sicherman mailde op 3
april 2013:"Making a rectangle from T pentominoes and square tetrominoes
is moderately hard. Making one from N pentominoes and square tetrominoes is
harder!"
Opgave
4
Bepaal een rechthoek die kan worden betegeld met de O-tetromino en de
N-pentomino.
George vond een oplossing met oppervlakte 160.
Kan je het beter?
Goede oplossers verwerven eeuwige roem.
Mail naar:
o.d.m@fulladsl.be
| Naam |
Land |
Opgave
4 |
| George Sicherman |
USA |
160 |
| Aad van de Wetering |
Nederland |
160 |
| Peter Jeuken |
Nederland |
160 |
| Martin Friedeman |
Nederland |
160 |
| Nico Looije |
Nederland |
160 |
Peter Jeuken: "De opgave heeft me nogal wat
tijd gekost. Ik heb ook lang zitten kijken naar het 14x14 vierkant van Aad.
Wat een prachtig patroon! Het lijkt wel kunst. Mijn oplossing voor de opgave
van George is een 8x20 rechthoek. Ik heb 2 extra kleuren gebruikt om de
grenzen tussen de N-pentomino's en de O-tetromino's onderling beter te doen
uitkomen."
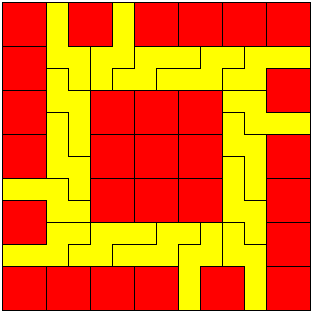
Aad stuurde ons dit mooie plaatje. Het kleinste vierkant met
N-pentomino's en O-tetromino's
Wil je toch heel graag onze oplossing zien stuur dan een mail.