Tiling
In 'Euclides' (the magazine of the Dutch Association of Mathematics Teachers
) in the magazine of April 2008 stood this
recreation pentominoes puzzle. The most joy you have when you
find him yourself, but we made use of the great program of Aad van de
Wetering Flat Poly that solves the problem incredibly fast.
Puzzle 1
Tile a rectangle with one or more copies of the
pentominoes and one or more copies of domino.
Try to make a rectangle with the smallest possible surface area.
Solve this puzzle for each of the pentominoes.

There are 12 problems to solve and the most are trivial.
The sum of the areas in our solution is 164.
Can you do better?
Good
solvers obtain eternal fame
Mail to:
o.d.m@fulladsl.be
| Name
|
Country |
Puzzle 1 |
| Frits Göbel |
The Netherlands |
158 |
| Aad van de Wetering |
The Netherlands |
163 |
| Helmut Postl |
Austria |
158 |
| Peter Jeuken |
The Netherlands |
158 |
| Lieke de Rooij |
The Netherlands |
158 |
|
Nico Looije |
The Netherlands |
158 |
Puzzle 2
Make a rectangle from Z pentominoes and I-trominoes.

We found a
solution with
area 42.
Can you do better?
Good
solvers obtain eternal fame
Mail to:
o.d.m@fulladsl.be
| Name |
Country |
Puzzle
2 |
| Aad van de Wetering |
The Netherlands |
42 |
| Helmut Postl |
Austria |
42 |
| Martin Friedeman |
The Netherlands |
42 |
| Peter Jeuken |
The Netherlands |
42 |
| Lieke de Rooij |
The Netherlands |
42 |
|
Nico Looije |
The Netherlands |
42 |
George Sicherman: "Here is a square solution"

Puzzle 3
Make a rectangle from T pentominoes and O-tetrominoes.

We found a
solution with
area 80.
Can you do better?
Good
solvers obtain eternal fame
Mail to:
o.d.m@fulladsl.be
|
Name |
Country |
Puzzle
3 |
| Aad van de Wetering |
The Netherlands |
80 |
| Helmut Postl |
Austria |
80 |
| Martin Friedeman |
The Netherlands |
80 |
| Peter Jeuken |
The Netherlands |
80 |
| Lieke de Rooij |
The Netherlands |
80 |
| George Sicherman |
US |
80 |
| Nico Looije |
The Netherlands |
80 |
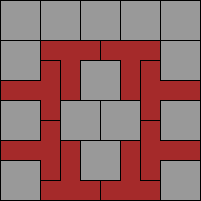
George
Sicherman:"Here is a complementary square for the T pentomino. (For
4-rotary symmetry, you will need a 14x14 square.)"
George Sicherman
emailed: "Making a rectangle from T pentominoes and square tetrominoes
is moderately hard. Making one from N pentominoes and square tetrominoes is
harder!"
Puzzle
4
Make a rectangle from N pentominoes and O-tetrominoes.
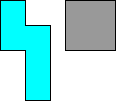
George found a
solution with
area 160.
Can you do better?
Good
solvers obtain eternal fame
Mail to:
o.d.m@fulladsl.be
|
Name |
Country |
Puzzle 4 |
| George Sicherman |
US |
160 |
| Aad van de Wetering |
The Netherlands |
160 |
| Peter Jeuken |
The Netherlands |
160 |
| Martin Friedeman |
The Netherlands |
160 |
| Nico Looije |
The Netherlands |
160 |
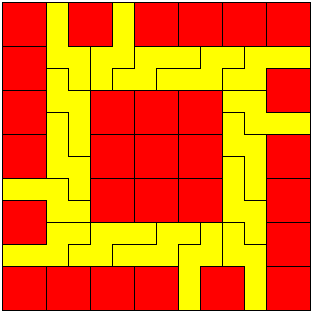
Aad
sent us this beautiful picture.
The smallest square with
N-pentominoes and O-tetrominoes
Do you
really like to see our solution? Send us
an email.