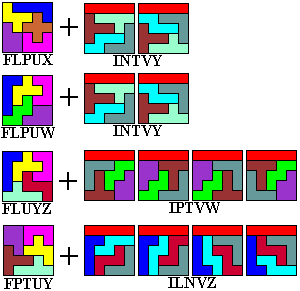
We kregen een mail van Leon van den Broek met de vraag of het mogelijk was met één set pentomino's twee vierkanten van 5x5 te maken.
Vooraleer we over FlatPoly (= schitterend programma van Aad van de Wetering) beschikten, hadden we (= 2 IW) alle vierkanten van 5x5 gezocht die we met een pentominoset konden leggen. Het zijn er 107.
Met de pentomino's kan men 792 groepjes maken van 5 verschillende.(Aantal combinaties van 12 elementen 5 per 5 genomen)
Hiervan zijn er echter maar 44 waarmee we een vierkant kunnen leggen.
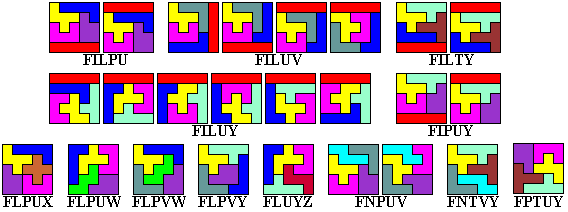
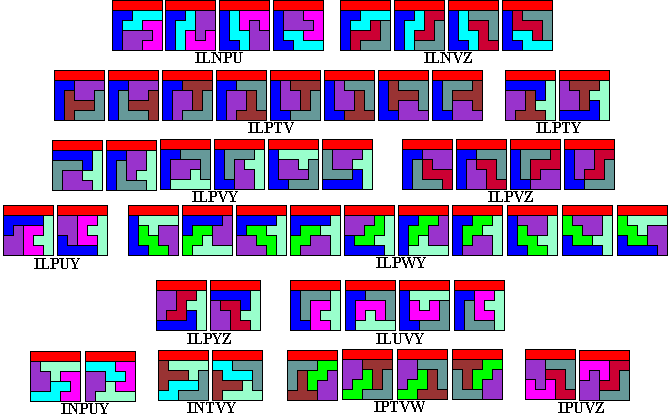
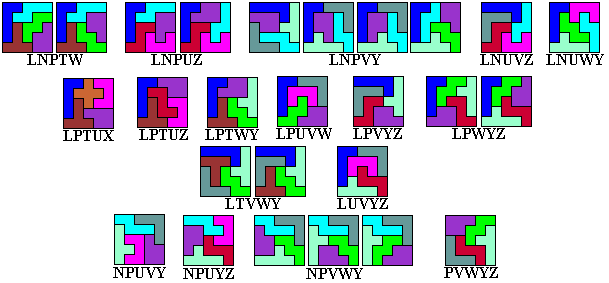
We bekijken deze mogelijkheden en kwamen tot het volgende resultaat: