Een vierkante cake met één hoekje af, is verdeeld in 7 ongelijke delen. Dit is gebeurd door te snijden volgens de rode, blauwe en groene lijn. Deze lijnen zijn op het raster getekend. Geen enkele lijn snijdt zichzelf en iedere lijn heeft juist één snijpunt met de andere.
Als je de voorgaande regels volgt, kan je de cake verdelen in 7 congruente delen met 3 lijnen?
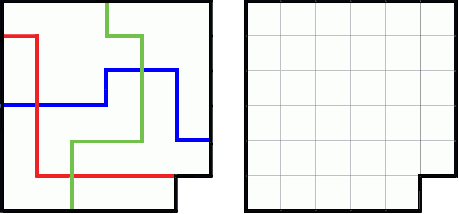
Er zijn 2 mogelijke oplossingen.
Goede oplossers verwerven eeuwige roem.
Mail naar: o.d.m@fulladsl.be