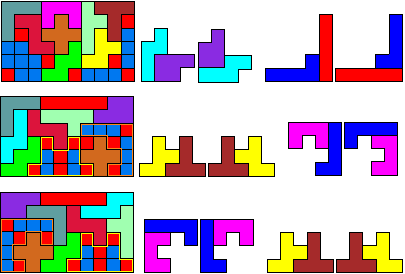
Dit puzzeltje is van Dion Gijswijt. We vonden het in Pythagoras van september 2008.
Hieronder zie je de twaalf pentomino's. Van elke pentomino zijn de uiteinden rood gekleurd.
Dit doet ons heel erg denken aan een set pentopijpen.
Vul de onderstaande 6x10 rechthoek met de twaalf pentomino's en wel zo, dat de 28 uiteindes op de aangegeven plaatsen terecht komen. Je mag de pentomino's draaien en spiegelen.

We begonnen met de X- en de I-pento te plaatsen.
Wil je de oplossing controleren, druk dan op de opgave.
Toen we Dion vroegen of we zijn puzzeltje mochten publiceren was zijn antwoord:"Leuk dat je m'n puzzel erbij hebt gezet! Zelf kwam ik heel anders op de oplossing, namelijk door de pentomino's vakje voor vakje binnen de rechthoek te reconstrueren. Als bij magie heb je dan aan het eind een pentomino-betegeling :)
Je hebt gelijk dat het lijkt op dat pijpen-idee, dat is ook leuk!
Jullie Pentomino site is zo langzamerhand DE pentomino-bron op internet aan het worden, ga zo door!"
Bedankt Dion.
Of het echter verstandig is van de oplossing te zoeken door een rechthoek van 10x6 te vullen met pentomino's denken we niet aangezien er 2339 verschillende oplossingen zijn.
We vroegen ons af of de 2339 verschillende vullingen ook 2339 verschillende betegelingen geven en gingen op zoek.
We vonden er zeker één: onderstaande betegeling heeft 2 oplossingen

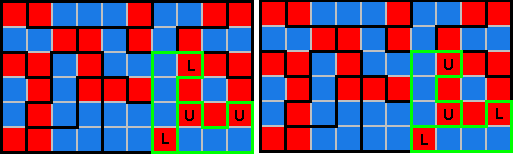
Kan je er nog vinden?
Mail naar: o.d.m@fulladsl.be
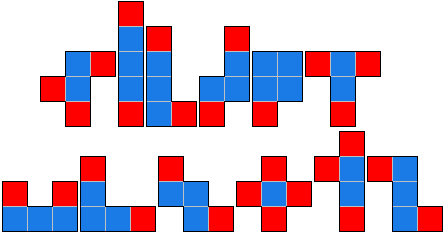
Onze eerste reactie kregen we van Aad:"Leuk probleem, ik had het een tijdje terug al opgelost. Het extraatje intrigeerde me, in de bijlage staan 3 series van 4 identiekelingen, als voorbeeld.
Meer dan 4 gelijke zijn niet mogelijk, van minder dan 4 zijn er heel wat."

We keken: