In juli 2009 kegen we een mail van Frits Gobel waarin het volgende stond:"Misschien vind je deze pentomino-puzzel leuk: probeer met twee setjes een zo groot mogelijke rechthoek met een (zo groot mogelijk) centraal gat te maken.
[Voor één setje is mijn rekord 8 bij 9 met een gat van 4 bij 3. Dat zal ongetwijfeld een bekend resultaat zijn.]"
We gingen onmiddellijk aan de slag met FlatPoly

Het beste resultaat dat we vonden was een rechthoek van 12x18 met een gat van 96 als tenminste het gat ook een rechthoek moest zijn.

We kregen een mail van Frits: "Wat een mooie oplossingen! Hoe heb je die zo snel gevonden...Het was inderdaad de bedoeling dat het gat rechthoekig moest zijn. Dus die van 12 bij 18 vind ik het allermooist! Ik heb de slimme combinaties van 'lastige' pentomino's met bewondering bekeken."
We hebben hem maar over FlatPoly verteld...
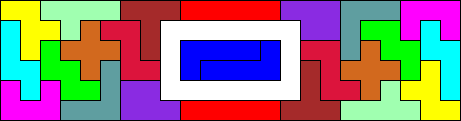
Maar we kunnen beter: een rechthoek van 16x14 met een gat van 104.
Wil je de oplossing zien? Klik hierboven.
Kan je nog beter? Mail het ons: o.d.m@fulladsl.be
George Sicherman kon beter:"Here is an even bigger hole with a double set of pentominoes."
Een rechthoek van 15x16 met een gat van 120.( 2 soorten oplossingen)
Wil je de oplossing zien? Klik hierboven.
George vond nog een andere oplossing: een rechthoek van 12x20 met een gat van 10x12
Wil je de oplossing zien? Klik hierboven.
We bekeken echter nog eens hetzelfde probleem met één set.
Frits was wel heel zeker van het record.

8x9 met gat van 12
We vonden echter beter

8x10 met gat van 20
En we kunnen nog beter: 8x11 met gat van 28
Wil je de oplossing zien? Klik hierboven.
Kan je nog beter? Mail het ons: o.d.m@fulladsl.be
George Sicherman: "8 x 11 is indeed the biggest with a single set of pentominoes." en nadien: "However ... 8 x 11 is not the longest rectangle! This one is 5 x 15."

En George bedacht nog een nieuw probleem: "What is the biggest hole in a hole in a rectangle? (Probably not this one.)"