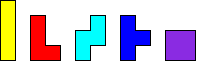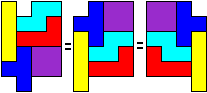Tetromino cilinder
Edo Timmermans
Je kan heel veel moois
vinden op Edo zijn Youtube kanaal:
https://www.youtube.com/user/EdoTimmermans?feature=mhee
De tetrominoset is gemaakt met ningboballs die je
kan aankopen op
http://www.ningboballs.eu/nl/
Je krijgt een set tetromino's
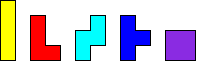
Met deze set kan je op 8 verschillende manieren de volgende vorm vullen.

Hieronder zie je hoe dit kan.

We rollen de vorm tot een buis. In het filmpje kan je dit heel goed zien.
Hierdoor ontstaan 6 verschillende cilinders (Er zijn er 2 keer 2 dezelfde
bij)
Er is echter nog een
mogelijkheid om de cilinder te maken en die oplossing kan niet herleid
worden tot de voorgaande vorm.
Kan je die vinden?


Martin Grider maakte een video met de volgende
oplossing

We leggen uit waarom dit geen nieuwe oplossing is en ze in de basisvorm
past:
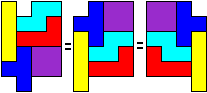
We kregen de oplossing van Helmut Postl toegestuurd met nog een mooie
bijkomende bedenking:
"Een interessant feit is dat er verschillende cilinders bestaan, maar geen
enkele andere dan de gegeven cilinder kan worden gemaakt met de tetromino's.
De gegeven cilinder heeft hoogte h = 4 en omtrek p = 5. In principe kunnen
we cilinders maken met h . p = 20, waarbij (h, p) = (1,20), (2,10), (4,5),
(5,4), (10,2 ) en (20,1). Omdat de tetromino's een oneven dambord pariteit
hebben, moet de omtrek oneven zijn. Hierdoor zijn alleen nog (4,5) en (20,1)
mogelijk, waarbij het laatste uiteraard niet kan worden gemaakt met de
tetromino's"
Het volgende plaatje verduidelijkt 'oneven dambord pariteit'

We gebruikten dit al eens eerder op onze "tetrominosite" die we maakten voor
Thinkquest (maar die jammer genoeg van het web verdwenen is).
We toonden ermee aan dat we met de tetromino's geen rechthoek kunnen leggen.
http://www.pentomino.classy.be/bestanden/thinkquest/rechthoeken/rechthoeken.html